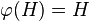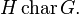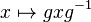Characteristic subgroup

In mathematics, particularly in the area of abstract algebra known as group theory, a characteristic subgroup is a subgroup that is invariant under all automorphisms of the parent group.^[1]^[2] Because conjugation is an automorphism, every characteristic subgroup is normal, though not every normal subgroup is characteristic. Examples of characteristic subgroups include the commutator subgroup and the center of a group.

Definitions

A characteristic subgroup of a group G is a subgroup H that is invariant under each automorphism of G. That is,

\varphi(H) = H

for every automorphism φ of G (where φ(H) denotes the image of H under φ).

The statement “H is a characteristic subgroup of G” is written

H\mathrel{{}\operatorname{char}{}}G.

Characteristic vs. normal

If G is a group, and g is a fixed element of G, then the conjugation map

x \mapsto g x g^{-1}

is an automorphism of G (known as an inner automorphism). A subgroup of G that is invariant under all inner automorphisms is called normal. Since a characteristic subgroup is invariant under all automorphisms, every characteristic subgroup is normal.

Not every normal subgroup is characteristic. Here are several examples:

Let H be a group, and let G be the direct product H × H. Then the subgroups {1} × H and H × {1} are both normal, but neither is characteristic. In particular, neither of these subgroups is invariant under the automorphism (x, y) → (y, x) that switches the two factors.
For a concrete example of this, let V be the Klein four-group (which is isomorphic to the direct product Z₂ × Z₂). Since this group is abelian, every subgroup is normal; but every permutation of the three non-identity elements is an automorphism of V, so the three subgroups of order 2 are not characteristic.Here 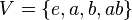$V=\left\{e,a,b,ab\right\}$ Consider H={e,a} and consider the automorphism 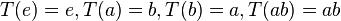$T(e)=e, T(a)=b, T(b)=a, T(ab)=ab$ .Then T(H) is not contained in H.
In the quaternion group of order 8, each of the cyclic subgroups of order 4 is normal, but none of these are characteristic. However, the subgroup {1, −1} is characteristic, since it is the only subgroup of order 2.

Note: If H is the unique subgroup of a group G, then H is characteristic in G.

If n is even, the dihedral group of order 2n has three subgroups of index two, all of which are normal. One of these is the cyclic subgroup, which is characteristic. The other two subgroups are dihedral; these are permuted by an outer automorphism of the parent group, and are therefore not characteristic.
"Normality" is not transitive, but Characteristic has a transitive property, namely if H Char K and K normal in G then H normal in G.

Comparison to other subgroup properties

Distinguished subgroups

A related concept is that of a distinguished subgroup (also called strictly characteristic subgroup). In this case the subgroup H is invariant under the applications of surjective endomorphisms. For a finite group this is the same, because surjectivity implies injectivity, but not for an infinite group: a surjective endomorphism is not necessarily an automorphism.

Fully invariant subgroups

For an even stronger constraint, a fully characteristic subgroup (also called a fully invariant subgroup) H of a group G is a group remaining invariant under every endomorphism of G; in other words, if f : G → G is any homomorphism, then f(H) is a subgroup of H.

Verbal subgroups

An even stronger constraint is verbal subgroup, which is the image of a fully invariant subgroup of a free group under a homomorphism.

Containments

Every subgroup that is fully characteristic is certainly distinguished and therefore characteristic; but a characteristic or even distinguished subgroup need not be fully characteristic.

The center of a group is always a distinguished subgroup, but it is not always fully characteristic. The finite group of order 12, Sym(3) × Z/2Z has a homomorphism taking (π, y) to ( (1,2)^y, 0) which takes the center 1 × Z/2Z into a subgroup of Sym(3) × 1, which meets the center only in the identity.

The relationship amongst these subgroup properties can be expressed as:

subgroup ⇐ normal subgroup ⇐ characteristic subgroup ⇐ distinguished subgroup ⇐ fully characteristic subgroup ⇐ verbal subgroup

Examples

Finite example

Consider the group G = S₃ × Z₂ (the group of order 12 which is the direct product of the symmetric group of order 6 and a cyclic group of order 2). The center of G is its second factor Z₂. Note that the first factor S₃ contains subgroups isomorphic to Z₂, for instance {identity,(12)}; let f: Z₂ → S₃ be the morphism mapping Z₂ onto the indicated subgroup. Then the composition of the projection of G onto its second factor Z₂, followed by f, followed by the inclusion of S₃ into G as its first factor, provides an endomorphism of G under which the image of the center Z₂ is not contained in the center, so here the center is not a fully characteristic subgroup of G.

Cyclic groups

Every subgroup of a cyclic group is characteristic.

Subgroup functors

The derived subgroup (or commutator subgroup) of a group is a verbal subgroup. The torsion subgroup of an abelian group is a fully invariant subgroup.

Topological groups

The identity component of a topological group is always a characteristic subgroup.

Transitivity

The property of being characteristic or fully characteristic is transitive; if H is a (fully) characteristic subgroup of K, and K is a (fully) characteristic subgroup of G, then H is a (fully) characteristic subgroup of G.

Moreover, while it is not true that every normal subgroup of a normal subgroup is normal, it is true that every characteristic subgroup of a normal subgroup is normal. Similarly, while it is not true that every distinguished subgroup of a distinguished subgroup is distinguished, it is true that every fully characteristic subgroup of a distinguished subgroup is distinguished.

Map on Aut and End

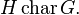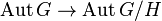If $H\,\mathrm{char}\,G.$ , then every automorphism of G induces an automorphism of the quotient group G/H, which yields a map $\mbox{Aut}\,G \to \mbox{Aut}\, G/H$ .

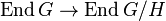If H is fully characteristic in G, then analogously, every endomorphism of G induces an endomorphism of G/H, which yields a map $\mbox{End}\,G \to \mbox{End}\, G/H$ .

References

↑ Dummit, David S.; Foote, Richard M. (2004). Abstract Algebra (3rd ed.). John Wiley & Sons. ISBN 0-471-43334-9.
↑ Lang, Serge (2002). Algebra. Graduate Texts in Mathematics. Springer. ISBN 0-387-95385-X.