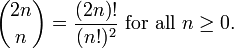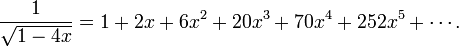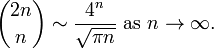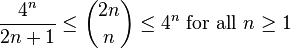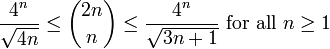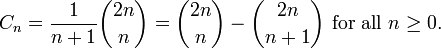Central binomial coefficient
In mathematics the nth central binomial coefficient is defined in terms of the binomial coefficient by
They are called central since they show up exactly in the middle of the even-numbered rows in Pascal's triangle. The first few central binomial coefficients starting at n = 0 are:
Properties
These numbers have the generating function
The Wallis product can be written in form of an asymptotic for the central binomial coefficient:
The latter can also be easily established by means of Stirling's formula. On the other hand, it can also be used as a means to determine the constant 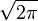 in front of the Stirling formula, by comparison.
in front of the Stirling formula, by comparison.
Simple bounds are given by
Some better bounds are
and, if more accuracy is required,
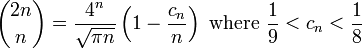 for all
for all 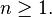
Related sequences
The closely related Catalan numbers Cn are given by:
A slight generalization of central binomial coefficients is to take them as
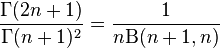 , with appropriate real numbers n, where
, with appropriate real numbers n, where 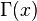 is Gamma function and
is Gamma function and 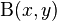 is Beta function.
is Beta function.
See also
References
- Koshy, Thomas (2008), Catalan Numbers with Applications, Oxford University Press, ISBN 978-0-19533-454-8.
External links
- Central binomial coefficient at PlanetMath.org.
- Binomial coefficient at PlanetMath.org.
- Pascal's triangle at PlanetMath.org.
- Catalan numbers at PlanetMath.org.
This article incorporates material from Central binomial coefficient on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.