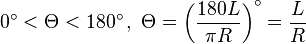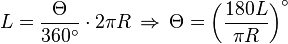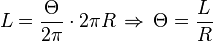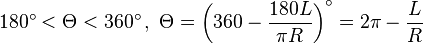Central angle

Angle AOB forms a central angle

A central angle is an angle whose apex (vertex) is the center O of a circle and whose legs (sides) are radii intersecting the circle in two distinct points A and B thereby subtending an arc between those two points whose angle is (by definition) equal to that of the central angle itself.^[1] It is also known as the arc segment's angular distance.

When defining or drawing a central angle, in addition to specifying the points A and B, one must specify and/or denote whether the angle being defined is the convex angle (<180°) or the reflex angle (>180°).

The size of a central angle Θ is: 0°<Θ<360° оr 0<Θ<2π (radians)

Formulas

If the intersection points A and B of the legs of the angle with the circle form a diameter, then Θ=180° is a straight angle. (In radians, Θ=π.)

Let L be the minor arc of the circle between points A and B, and let R be the radius of the circle.^[2]


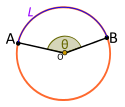Central angle. Convex. Includes minor arc L

If the central angle Θ includes L, then

 $0^{\circ} < \Theta < 180^{\circ} \, , \,\, \Theta = \left( {\frac{180L}{\pi R}} \right) ^{\circ}=\frac{L}{R}$

Proof (for degrees): The circumference of a circle with radius R is: 2πR, and the minor arc L is the (^Θ/_360°) proportional part of the whole circumference (see arc). So:

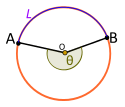L=\frac{\Theta}{360^{\circ}} \cdot 2 \pi R \, \Rightarrow \, \Theta = \left( {\frac{180L}{\pi R}} \right) ^{\circ}


Central angle. Reflex. Does not include L

Proof (for radians): The circumference of a circle with radius R is: 2πR, and the minor arc L is the (^Θ/_2π) proportional part of the whole circumference (see arc). So:

L=\frac{\Theta}{2 \pi} \cdot 2 \pi R \, \Rightarrow \, \Theta = \frac{L}{R}

If the central angle Θ does not include the minor arc L, then the Θ is a reflex angle and:

 $180^{\circ} < \Theta < 360^{\circ} \, , \,\, \Theta = \left( 360 - \frac{180L}{\pi R} \right) ^{\circ}=2\pi-\frac{L}{R}$

If a tangent at A and a tangent at B intersect at the exterior point P, then denoting the centre as O, the angles ∠BOA (convex) and ∠BPA are supplementary (sum to 180 °).

References

↑ Clapham, C.; Nicholson, J. (2009). "Oxford Concise Dictionary of Mathematics, Central Angle". Addison-Wesley. p. 122. Retrieved December 2013.
↑ "Central angle (of a circle)". Math Open Reference. 2009. Retrieved December 2013. interactive

External links

"Central angle (of a circle)". Math Open Reference. 2009. Retrieved December 2013. interactive
"Central Angle Theorem". Math Open Reference. 2009. Retrieved December 2013. interactive
Inscribed and Central Angles in a Circle

Central angle

Formulas

See also

References

External links