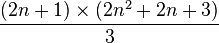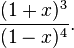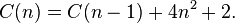Centered octahedral number

Haüy construction of an octahedron by 129 cubes

A centered octahedral number or Haüy octahedral number is a figurate number that counts the number of points of a three-dimensional integer lattice that lie inside an octahedron centered at the origin.[1] The same numbers are special cases of the Delannoy numbers, which count certain two-dimensional lattice paths.[2] The Haüy octahedral numbers are named after René Just Haüy.

History

The name "Haüy octahedral number" comes from the work of René Just Haüy, a French mineralogist active in the late 18th and early 19th centuries. His "Haüy construction" approximates an octahedron as a polycube, formed by accreting concentric layers of cubes onto a central cube. The centered octahedral numbers count the number of cubes used by this construction.[3] Haüy proposed this construction, and several related constructions of other polyhedra, as a model for the structure of crystalline minerals.[4][5]

Formula

The number of three-dimensional lattice points within n steps of the origin is given by the formula

\frac{(2n+1)\times(2n^2+2n+3)}{3}

The first few of these numbers (for n = 0, 1, 2, ...) are

1, 7, 25, 63, 129, 231, 377, 575, 833, 1159, …[6]

The generating function of the centered octahedral numbers is[6][7]

\frac{(1+x)^3}{(1-x)^4}.

The centered octahedral numbers obey the recurrence relation[1]

C(n)=C(n-1)+4n^2+2.

They may also be computed as the sums of pairs of consecutive octahedral numbers.

Alternative interpretations

63 Delannoy paths through a 3 × 3 grid

The octahedron in the three-dimensional integer lattice, whose number of lattice points is counted by the centered octahedral number, is a metric ball for three-dimensional taxicab geometry, a geometry in which distance is measured by the sum of the coordinatewise distances rather than by Euclidean distance. For this reason, Luther & Mertens (2011) call the centered octahedral numbers "the volume of the crystal ball".[7]

The same numbers can be viewed as figurate numbers in a different way, as the centered figurate numbers generated by a pentagonal pyramid. That is, if one forms a sequence of concentric shells in three dimensions, where the first shell consists of a single point, the second shell consists of the six vertices of a pentagonal pyramid, and each successive shell forms a larger pentagonal pyramid with a triangular number of points on each triangular face and a pentagonal number of points on the pentagonal face, then the total number of points in this configuration is a centered octahedral number.[1]

The centered octahedral numbers are also the Delannoy numbers of the form D(3,n). As for Delannoy numbers more generally, these numbers count the number of paths from the southwest corner of a 3 × n grid to the northeast corner, using steps that go one unit east, north, or northeast.[2]

References

  1. ↑ 1.0 1.1 1.2 Deza, Elena; Deza, Michel (2012), Figurate Numbers, World Scientific, pp. 107–109, 132, ISBN 9789814355483.
  2. ↑ 2.0 2.1 Sulanke, Robert A. (2003), "Objects counted by the central Delannoy numbers" (PDF), Journal of Integer Sequences 6 (1), Article 03.1.5, MR 1971435.
  3. ↑ Fathauer, Robert W. (2013), "Iterative arrangements of polyhedra – Relationships to classical fractals and Haüy constructions", Proceedings of Bridges 2013: Mathematics, Music, Art, Architecture, Culture (PDF)
  4. ↑ Maitte, Bernard (2013), "The Construction of Group Theory in Crystallography", in Barbin, Evelyne; Pisano, Raffaele, The Dialectic Relation Between Physics and Mathematics in the XIXth Century, History of Mechanism and Machine Science 16, Springer, pp. 1–30, doi:10.1007/978-94-007-5380-8_1, ISBN 9789400753808. See in particular p. 10.
  5. ↑ Haüy, René-Just (1784), Essai d'une théorie sur la structure des crystaux (in French). See in particular pp. 13–14. As cited by Weisstein, Eric W., "Haűy [sic] Construction", MathWorld.
  6. ↑ 6.0 6.1 "Sloane's A001845 : Centered octahedral numbers (crystal ball sequence for cubic lattice)", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
  7. ↑ 7.0 7.1 Luther, Sebastian; Mertens, Stephan (2011), "Counting lattice animals in high dimensions", Journal of Statistical Mechanics: Theory and Experiment 2011 (9): P09026, arXiv:1106.1078