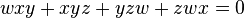Cayley's nodal cubic surface

Not to be confused with Cayley's ruled cubic surface.

Real points of the Cayley surface

In algebraic geometry, the Cayley surface, named after Arthur Cayley, is a cubic nodal surface in 3-dimensional projective space with four conical points. It can be given by the equation

wxy+ xyz+ yzw+zwx =0\

when the four singular points are those with three vanishing coordinates. Changing variables gives several other simple equations defining the Cayley surface.

References

Cayley, Arthur (1869), "A Memoir on Cubic Surfaces", Philosophical Transactions of the Royal Society of London (The Royal Society) 159: 231–326, doi:10.1098/rstl.1869.0010, ISSN 0080-4614, JSTOR 108997
Heath-Brown, D. R. (2003), "The density of rational points on Cayley's cubic surface", Proceedings of the Session in Analytic Number Theory and Diophantine Equations, Bonner Math. Schriften 360, Bonn: Univ. Bonn, p. 33, MR 2075628
Hunt, Bruce (2000), "Nice modular varieties", Experimental Mathematics 9 (4): 613–622, doi:10.1080/10586458.2000.10504664, ISSN 1058-6458, MR R1806296

External links

Endraß, Stephan (2003), The Cayley cubic
Surface de Cayley
Weisstein, Eric W., "Cayley cubic", MathWorld.