Cayley's formula

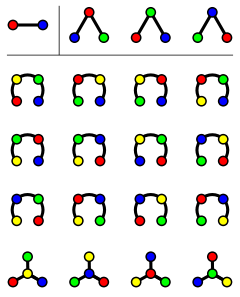
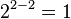The complete list of all trees on 2,3,4 labeled vertices: 2^{2-2}=1 tree with 2 vertices, 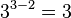3^{3-2}=3 trees with 3 vertices and 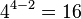4^{4-2}=16 trees with 4 vertices.

In mathematics, Cayley's formula is a result in graph theory named after Arthur Cayley. It states that for every positive integer n, the number of trees on n labeled vertices is 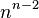n^{n-2}.

The formula equivalently counts the number of spanning trees of a complete graph with labeled vertices (sequence A000272 in OEIS).

Proof

Many remarkable proofs of Cayley's tree formula are known.[1] One classical proof of the formula uses Kirchhoff's matrix tree theorem, a formula for the number of spanning trees in an arbitrary graph involving the determinant of a matrix. Prüfer sequences yield a bijective proof of Cayley's formula. Another bijective proof, by André Joyal, finds a one-to-one transformation between n-node trees with two distinguished nodes and maximal directed pseudoforests. A proof by double counting due to Jim Pitman counts in two different ways the number of different sequences of directed edges that can be added to an empty graph on n vertices to form from it a rooted tree; see Double counting (proof technique)#Counting trees.

History

The formula was first discovered by Carl Wilhelm Borchardt in 1860, and proved via a determinant.[2] In a short 1889 note, Cayley extended the formula in several directions, by taking into account the degrees of the vertices.[3] Although he referred to Borchardt's original paper, the name "Cayley's formula" became standard in the field.

References

  1. ↑ Aigner, Martin; Ziegler, Günter M. (1998). Proofs from THE BOOK. Springer-Verlag. pp. 141–146.
  2. ↑ Borchardt, C. W. (1860). "Über eine Interpolationsformel für eine Art Symmetrischer Functionen und über Deren Anwendung". Math. Abh. der Akademie der Wissenschaften zu Berlin: 1–20.
  3. ↑ Cayley, A. (1889). "A theorem on trees". Quart. J. Math 23: 376–378.