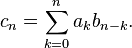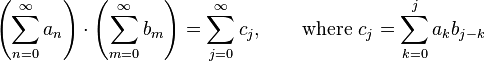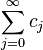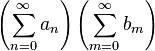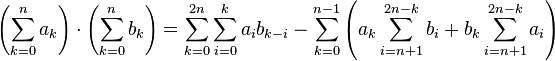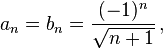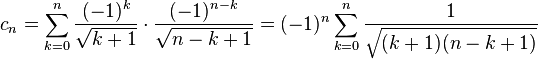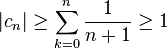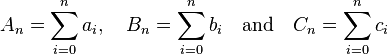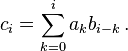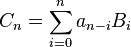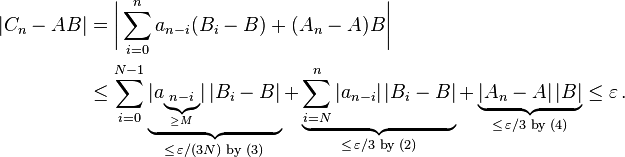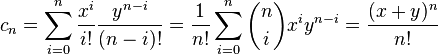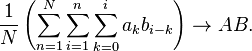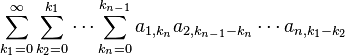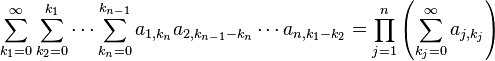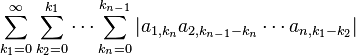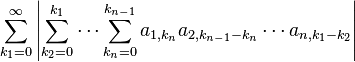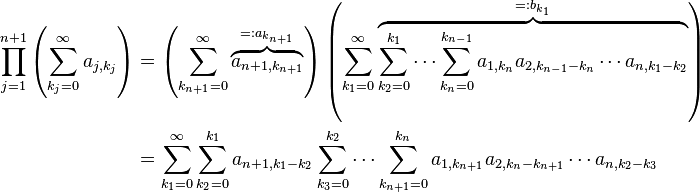Cauchy product

In mathematics, the Cauchy product, named after Augustin Louis Cauchy, of two sequences 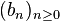$\textstyle (a_n)_{n\geq0}$ , $\textstyle (b_n)_{n\geq0}$ , is the discrete convolution of the two sequences, the sequence 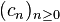$\textstyle (c_n)_{n\geq0}$ whose general term is given by

c_n=\sum_{k=0}^n a_k b_{n-k}.

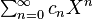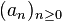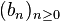In other words, it is the sequence whose associated formal power series $\textstyle \sum_{n=0}^\infty c_nX^n$ is the product of the two series similarly associated to $(a_n)_{n\geq0}$ and $(b_n)_{n\geq0}$ .

Series

A particularly important example is to consider the sequences 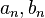$\textstyle a_n, b_n$ to be terms of two strictly formal (not necessarily convergent) series

\sum_{n=0}^\infty a_n,\qquad \sum_{n=0}^\infty b_n,

usually, of real or complex numbers. Then the Cauchy product is defined by a discrete convolution as follows.

\left(\sum_{n=0}^\infty a_n\right) \cdot \left(\sum_{m=0}^\infty b_m\right) = \sum_{j=0}^\infty c_j,\qquad\mathrm{where}\ c_j=\sum_{k=0}^j a_k b_{j-k}

for n = 0, 1, 2, ...

"Formal" means we are manipulating series in disregard of any questions of convergence. These need not be convergent series. See in particular formal power series.

One hopes, by analogy with finite sums, that in cases in which the two series do actually converge, the sum of the infinite series

\sum_{j=0}^\infty c_j

is equal to the product

\left(\sum_{n=0}^\infty a_n\right) \left(\sum_{m=0}^\infty b_m\right)

just as would work when each of the two sums being multiplied has only finitely many terms. This is not true in general, but see Mertens' Theorem and Cesàro's theorem below for some special cases.

Finite summations

The product of two finite series a_k and b_k with k between 0 and n satisfies the equation:

\left(\sum_{k=0}^{n} a_k\right) \cdot \left(\sum_{k=0}^{n} b_k\right)=\sum_{k=0}^{2n} \sum_{i=0}^k a_ib_{k-i} - \sum_{k=0}^{n-1} \left(a_k \sum_{i=n+1}^{2n-k}b_i +b_k \sum_{i=n+1}^{2n-k} a_i\right)

Convergence and Mertens' theorem

Not to be confused with Mertens' theorems concerning distribution of prime numbers.

Let $(a n) n \geq0$ and $(b n) n \geq0$ be real or complex sequences. It was proved by Franz Mertens that, if the series 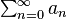$\textstyle \sum_{n=0}^\infty a_n$ converges to $A$ and 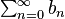$\textstyle \sum_{n=0}^\infty b_n$ converges to $B$ , and at least one of them converges absolutely, then their Cauchy product converges to $AB$ .

It is not sufficient for both series to be convergent; if both sequences are conditionally convergent, the Cauchy product does not have to converge towards the product of the two series, as the following example shows:

Example

Consider the two alternating series with

a_n = b_n = \frac{(-1)^n}{\sqrt{n+1}}\,,

which are only conditionally convergent (the divergence of the series of the absolute values follows from the direct comparison test and the divergence of the harmonic series). The terms of their Cauchy product are given by

c_n = \sum_{k=0}^n \frac{(-1)^k}{\sqrt{k+1}} \cdot \frac{ (-1)^{n-k} }{ \sqrt{n-k+1} } = (-1)^n \sum_{k=0}^n \frac{1}{ \sqrt{(k+1)(n-k+1)} }

for every integer $n \geq 0$ . Since for every $k \in {0, 1, ..., n}$ we have the inequalities $k + 1 \leq n + 1$ and $n - k + 1 \leq n + 1$ , it follows for the square root in the denominator that $\sqrt (k + 1)(n - k + 1) \leq n +1$ , hence, because there are $n + 1$ summands,

|c_n| \ge \sum_{k=0}^n \frac{1}{n+1} \ge 1

for every integer $n \geq 0$ . Therefore, $c n$ does not converge to zero as $n \to \infty$ , hence the series of the $(c n) n \geq0$ diverges by the term test.

Proof of Mertens' theorem

Assume without loss of generality that the series of the 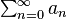$\textstyle \sum_{n=0}^\infty a_n$ converges absolutely. Define the partial sums

A_n = \sum_{i=0}^n a_i,\quad B_n = \sum_{i=0}^n b_i\quad\text{and}\quad C_n = \sum_{i=0}^n c_i

with

c_i=\sum_{k=0}^ia_kb_{i-k}\,.

Then

C_n = \sum_{i=0}^n a_{n-i}B_i

by rearrangement, hence

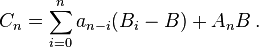
$C_n = \sum_{i=0}^na_{n-i}(B_i-B)+A_nB\,.$

(1)

Fix $ε > 0$ . Since 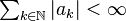$\textstyle \sum_{k\in{\mathbb N}} |a_k|<\infty$ by absolute convergence, and since $B n$ converges to $B$ as $n \to \infty$ , there exists an integer $N$ such that, for all integers $n \geq N$ ,

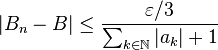
$|B_n-B|\le\frac{\varepsilon/3}{\sum_{ k\in{\mathbb N} } |a_k|+1}$

(2)

(this is the only place where the absolute convergence is used). Since the series of the $(a n) n \geq0$ converges, the individual $a n$ must converge to 0 by the term test. Hence there exists an integer $M$ such that, for all integers $n \geq M$ ,

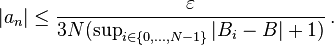
$|a_n|\le\frac{\varepsilon}{3N(\sup_{ i\in\{0,\dots,N-1\} } |B_i-B|+1)}\,.$

(3)

Also, since $A n$ converges to $A$ as $n \to \infty$ , there exists an integer $L$ such that, for all integers $n \geq L$ ,

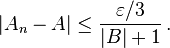
$|A_n-A|\le\frac{\varepsilon/3}{|B|+1}\,.$

(4)

Then, for all integers $n \geq max{L, M + N}$ , use the representation (1) for $C n$ , split the sum in two parts, use the triangle inequality for the absolute value, and finally use the three estimates (2), (3) and (4) to show that

\begin{align} |C_n - AB| &= \biggl|\sum_{i=0}^n a_{n-i}(B_i-B)+(A_n-A)B\biggr| \\ &\le \sum_{i=0}^{N-1}\underbrace{|a_{\underbrace{\scriptstyle n-i}_{\scriptscriptstyle \ge M}}|\,|B_i-B|}_{\le\,\varepsilon/(3N)\text{ by (3)}}+{}\underbrace{\sum_{i=N}^n |a_{n-i}|\,|B_i-B|}_{\le\,\varepsilon/3\text{ by (2)}}+{}\underbrace{|A_n-A|\,|B|}_{\le\,\varepsilon/3\text{ by (4)}}\le\varepsilon\,. \end{align}

By the definition of convergence of a series, $C n \to AB$ as required.

Examples

Finite series

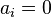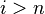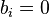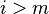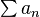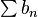Suppose $\textstyle a_i = 0$ for all $i>n$ and $\textstyle b_i = 0$ for all $\textstyle i>m$ . Here the Cauchy product of $\textstyle \sum a_n$ and $\textstyle \sum b_n$ is readily verified to be 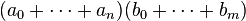$\textstyle (a_0+\cdots + a_n)(b_0+\cdots+b_m)$ . Therefore, for finite series (which are finite sums), Cauchy multiplication is direct multiplication of those series.

Infinite series

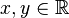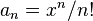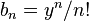For some $\textstyle x,y\in\mathbb{R}$ , let $\textstyle a_n = x^n/n!\,$ and $\textstyle b_n = y^n/n!\,$ . Then

c_n = \sum_{i=0}^n\frac{x^i}{i!}\frac{y^{n-i}}{(n-i)!} = \frac{1}{n!}\sum_{i=0}^n\binom{n}{i}x^i y^{n-i} = \frac{(x+y)^n}{n!}

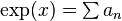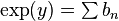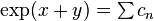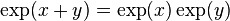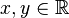by definition and the binomial formula. Since, formally, $\textstyle \exp(x) = \sum a_n$ and $\textstyle \exp(y) = \sum b_n$ , we have shown that $\textstyle \exp(x+y) = \sum c_n$ . Since the limit of the Cauchy product of two absolutely convergent series is equal to the product of the limits of those series, we have proven the formula $\textstyle \exp(x+y) = \exp(x)\exp(y)$ for all $\textstyle x,y\in\mathbb{R}$ .

As a second example, let 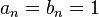$\textstyle a_n=b_n = 1$ for all 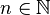$\textstyle n\in\mathbb{N}$ . Then 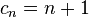$\textstyle c_n = n+1$ for all 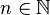$n\in\mathbb{N}$ so the Cauchy product 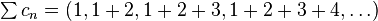$\textstyle \sum c_n = (1,1+2,1+2+3,1+2+3+4,\dots)$ does not converge.

Cesàro's theorem

In cases where the two sequences are convergent but not absolutely convergent, the Cauchy product is still Cesàro summable. Specifically:

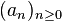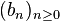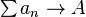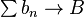If $\textstyle (a_n)_{n\geq0}$ , $\textstyle (b_n)_{n\geq0}$ are real sequences with $\textstyle \sum a_n\to A$ and $\textstyle \sum b_n\to B$ then

\frac{1}{N}\left(\sum_{n=1}^N\sum_{i=1}^n\sum_{k=0}^i a_k b_{i-k}\right)\to AB.

This can be generalised to the case where the two sequences are not convergent but just Cesàro summable:

Theorem

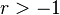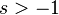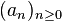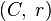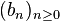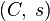For $\textstyle r>-1$ and $\textstyle s>-1$ , suppose the sequence $\textstyle (a_n)_{n\geq0}$ is $\textstyle (C,\; r)$ summable with sum A and $\textstyle (b_n)_{n\geq0}$ is $\textstyle (C,\; s)$ summable with sum B. Then their Cauchy product is 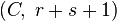$\textstyle (C,\; r+s+1)$ summable with sum AB.

Generalizations

All of the foregoing applies to sequences in 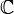$\textstyle \mathbb{C}$ (complex numbers). The Cauchy product can be defined for series in the 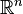$\textstyle \mathbb{R}^n$ spaces (Euclidean spaces) where multiplication is the inner product. In this case, we have the result that if two series converge absolutely then their Cauchy product converges absolutely to the inner product of the limits.

Products of finitely many infinite series

Let 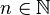$n \in \mathbb N$ such that 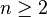$n \ge 2$ (actually the following is also true for 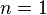$n=1$ but the statement becomes trivial in that case) and let 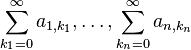$\sum_{k_1 = 0}^\infty a_{1, k_1}, \ldots, \sum_{k_n = 0}^\infty a_{n, k_n}$ be infinite series with complex coefficients, from which all except the $n$ th one converge absolutely, and the $n$ th one converges. Then the series

\sum_{k_1 = 0}^\infty \sum_{k_2 = 0}^{k_1} \cdots \sum_{k_n = 0}^{k_{n-1}} a_{1, k_n} a_{2, k_{n-1} - k_n} \cdots a_{n, k_1 - k_2}

converges and we have:

\sum_{k_1 = 0}^\infty \sum_{k_2 = 0}^{k_1} \cdots \sum_{k_n = 0}^{k_{n-1}} a_{1, k_n} a_{2, k_{n-1} - k_n} \cdots a_{n, k_1 - k_2} = \prod_{j=1}^n \left( \sum_{k_j = 0}^\infty a_{j, k_j} \right)

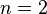This statement can be proven by induction over $n$ : The case for $n = 2$ is identical to the claim about the Cauchy product. This is our induction base.

The induction step goes as follows: Let the claim be true for an 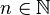$n \in \mathbb N$ such that 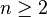$n \ge 2$ , and let 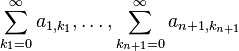$\sum_{k_1 = 0}^\infty a_{1, k_1}, \ldots, \sum_{k_{n+1} = 0}^\infty a_{n+1, k_{n+1}}$ be infinite series with complex coefficients, from which all except the 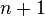$n+1$ th one converge absolutely, and the 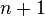$n+1$ th one converges. We first apply the induction hypothesis to the series 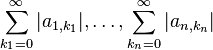$\sum_{k_1 = 0}^\infty |a_{1, k_1}|, \ldots, \sum_{k_n = 0}^\infty |a_{n, k_n}|$ . We obtain that the series

\sum_{k_1 = 0}^\infty \sum_{k_2 = 0}^{k_1} \cdots \sum_{k_n = 0}^{k_{n-1}} |a_{1, k_n} a_{2, k_{n-1} - k_n} \cdots a_{n, k_1 - k_2}|

converges, and hence, by the triangle inequality and the sandwich criterion, the series

\sum_{k_1 = 0}^\infty \left| \sum_{k_2 = 0}^{k_1} \cdots \sum_{k_n = 0}^{k_{n-1}} a_{1, k_n} a_{2, k_{n-1} - k_n} \cdots a_{n, k_1 - k_2} \right|

converges, and hence the series

\sum_{k_1 = 0}^\infty \sum_{k_2 = 0}^{k_1} \cdots \sum_{k_n = 0}^{k_{n-1}} a_{1, k_n} a_{2, k_{n-1} - k_n} \cdots a_{n, k_1 - k_2}

converges absolutely. Therefore, by the induction hypothesis, by what Mertens proved, and by renaming of variables, we have:

\begin{align} \prod_{j=1}^{n+1} \left( \sum_{k_j = 0}^\infty a_{j, k_j} \right) & = \left( \sum_{k_{n+1} = 0}^\infty \overbrace{a_{n+1, k_{n+1}}}^{=:a_{k_{n+1}}} \right) \left( \sum_{k_1 = 0}^\infty \overbrace{\sum_{k_2 = 0}^{k_1} \cdots \sum_{k_n = 0}^{k_{n-1}} a_{1, k_n} a_{2, k_{n-1} - k_n} \cdots a_{n, k_1 - k_2}}^{=:b_{k_1}} \right) \\ & = \sum_{k_1 = 0}^\infty \sum_{k_2 = 0}^{k_1} a_{n+1, k_1 - k_2} \sum_{k_3 = 0}^{k_2} \cdots \sum_{k_{n+1} = 0}^{k_n} a_{1, k_{n+1}} a_{2, k_n - k_{n+1}} \cdots a_{n, k_2 - k_3} \end{align}

Therefore, the formula also holds for 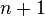$n+1$ .

Relation to convolution of functions

One can also define the Cauchy product of doubly infinite sequences, thought of as functions on 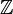$\textstyle \Z$ . In this case the Cauchy product is not always defined: for instance, the Cauchy product of the constant sequence 1 with itself, 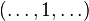$\textstyle (\dots,1,\dots)$ is not defined. This doesn't arise for singly infinite sequences, as these have only finite sums.

One has some pairings, for instance the product of a finite sequence with any sequence, and the product 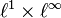$\textstyle \ell^1 \times \ell^\infty$ . This is related to duality of L^p spaces.

References

Apostol, Tom M. (1974), Mathematical Analysis (2nd ed.), Addison Wesley, p. 204, ISBN 978-0-201-00288-1
Hardy, G. H. (1949), Divergent Series, Oxford University Press, p. 227–229