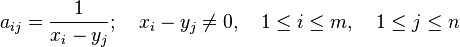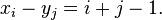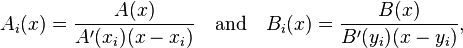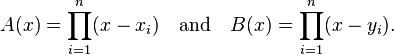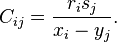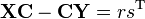Cauchy matrix
In mathematics, a Cauchy matrix, named after Augustin Louis Cauchy, is an m×n matrix with elements aij in the form
where 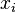 and
and 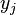 are elements of a field
are elements of a field  , and
, and 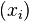 and
and 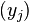 are injective sequences (they do not contain repeated elements; elements are distinct).
are injective sequences (they do not contain repeated elements; elements are distinct).
The Hilbert matrix is a special case of the Cauchy matrix, where
Every submatrix of a Cauchy matrix is itself a Cauchy matrix.
Cauchy determinants
The determinant of a Cauchy matrix is clearly a rational fraction in the parameters 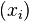 and
and 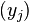 . If the sequences were not injective, the determinant would vanish, and tends to infinity if some
. If the sequences were not injective, the determinant would vanish, and tends to infinity if some 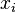 tends to
tends to 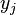 . A subset of its zeros and poles are thus known. The fact is that there are no more zeros and poles:
. A subset of its zeros and poles are thus known. The fact is that there are no more zeros and poles:
The determinant of a square Cauchy matrix A is known as a Cauchy determinant and can be given explicitly as
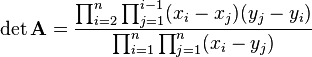 (Schechter 1959, eqn 4).
(Schechter 1959, eqn 4).
It is always nonzero, and thus all square Cauchy matrices are invertible. The inverse A−1 = B = [bij] is given by
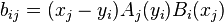 (Schechter 1959, Theorem 1)
(Schechter 1959, Theorem 1)
where Ai(x) and Bi(x) are the Lagrange polynomials for 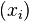 and
and 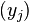 , respectively. That is,
, respectively. That is,
with
Generalization
A matrix C is called Cauchy-like if it is of the form
Defining X=diag(xi), Y=diag(yi), one sees that both Cauchy and Cauchy-like matrices satisfy the displacement equation
(with 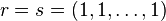 for the Cauchy one). Hence Cauchy-like matrices have a common displacement structure, which can be exploited while working with the matrix. For example, there are known algorithms in literature for
for the Cauchy one). Hence Cauchy-like matrices have a common displacement structure, which can be exploited while working with the matrix. For example, there are known algorithms in literature for
- approximate Cauchy matrix-vector multiplication with
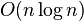 ops (e.g. the fast multipole method),
ops (e.g. the fast multipole method), - (pivoted) LU factorization with
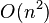 ops (GKO algorithm), and thus linear system solving,
ops (GKO algorithm), and thus linear system solving, - approximated or unstable algorithms for linear system solving in
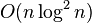 .
.
Here  denotes the size of the matrix (one usually deals with square matrices, though all algorithms can be easily generalized to rectangular matrices).
denotes the size of the matrix (one usually deals with square matrices, though all algorithms can be easily generalized to rectangular matrices).
See also
References
- A. Gerasoulis (1988). "A fast algorithm for the multiplication of generalized Hilbert matrices with vectors". Mathematics of Computation 50 (181): 179–188. doi:10.2307/2007921.
- I. Gohberg, T. Kailath, V. Olshevsky (1995). "Fast Gaussian elimination with partial pivoting for matrices with displacement structure". Mathematics of Computation 64 (212): 1557–1576. doi:10.1090/s0025-5718-1995-1312096-x.
- P. G. Martinsson, M. Tygert, V. Rokhlin (2005).
 . Computers & Mathematics with Applications 50: 741–752. doi:10.1016/j.camwa.2005.03.011.
. Computers & Mathematics with Applications 50: 741–752. doi:10.1016/j.camwa.2005.03.011. - S. Schechter (1959). "On the inversion of certain matrices". Mathematical Tables and Other Aids to Computation 13 (66): 73–77. doi:10.2307/2001955.