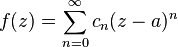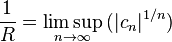Cauchy–Hadamard theorem

In mathematics, the Cauchy–Hadamard theorem is a result in complex analysis named after the French mathematicians Augustin Louis Cauchy and Jacques Hadamard, describing the radius of convergence of a power series. It was published in 1821 by Cauchy,^[1] but remained relatively unknown until Hadamard rediscovered it.^[2] Hadamard's first publication of this result was in 1888;^[3] he also included it as part of his 1892 Ph.D. thesis.^[4]

Theory for one complex variable

Statement of the theorem

Consider the formal power series in one complex variable z of the form

f(z) = \sum_{n = 0}^{\infty} c_{n} (z-a)^{n}

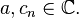
where $a,c_n\in\mathbb{C}.$

Then the radius of convergence of ƒ at the point a is given by

\frac{1}{R} = \limsup_{n \to \infty} \big( | c_{n} |^{1/n} \big)

where lim sup denotes the limit superior, the limit as n approaches infinity of the supremum of the sequence values after the nth position. If the sequence values are unbounded so that the lim sup is ∞, then the power series does not converge near a, while if the lim sup is 0 then the radius of convergence is ∞, meaning that the series converges on the entire plane.

Proof of the theorem

^[5] Without loss of generality assume that 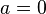$a=0$ . We will show first that the power series 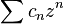$\sum c_n z^n$ converges for 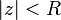$|z|<R$ , and then that it diverges for $|z|>R$ .

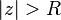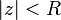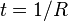First suppose $|z|<R$ . Let $t=1/R$ not be zero or ±infinity. For any 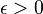$\epsilon > 0$ , there exists only a finite number of $n$ such that
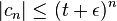$\sqrt[n]{|c_n|}\geq t+\epsilon$ . Now $|c_n|\leq(t+\epsilon)^n$ for all but a finite number of 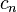$c_n$ , so the series 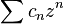$\sum c_n z^n$ converges if 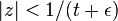$|z| < 1/(t+\epsilon)$ . This proves the first part.

Conversely, for 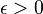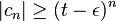$\epsilon > 0$ , $|c_n|\geq (t-\epsilon)^n$ for infinitely many 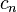$c_n$ , so if 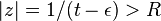$|z|=1/(t-\epsilon) > R$ , we see that the series cannot converge because its nth term does not tend to 0. Quod erat demonstrandum.

Several complex variables

Statement of the theorem

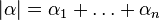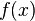Let $\alpha$ be a multi-index (a n-tuple of integers) with $|\alpha|=\alpha_1+\ldots+\alpha_n$ , then $f(x)$ converges with radius of convergence $\rho$ (which is also a multi-index) if and only if

$\lim_{|\alpha|\to\infty} \sqrt[|\alpha|]{|c_\alpha|\rho^\alpha}=1$

to the multidimensional power series

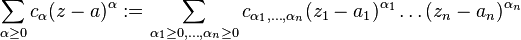
$\sum_{\alpha\geq0}c_\alpha(z-a)^\alpha := \sum_{\alpha_1\geq0,\ldots,\alpha_n\geq0}c_{\alpha_1,\ldots,\alpha_n}(z_1-a_1)^{\alpha_1}\ldots(z_n-a_n)^{\alpha_n}$

Proof of the theorem

The proof can be found in the book Introduction to Complex Analysis Part II functions in several Variables by B.V.Shabat

Notes

↑ Cauchy, A. L. (1821), Analyse algébrique .
↑ Bottazzini, Umberto (1986), The Higher Calculus: A History of Real and Complex Analysis from Euler to Weierstrass, Springer-Verlag, pp. 116–117, ISBN 978-0-387-96302-0 . Translated from the Italian by Warren Van Egmond.
↑ Hadamard, J., "Sur le rayon de convergence des séries ordonnées suivant les puissances d'une variable", C. R. Acad. Sci. Paris 106: 259–262 .
↑ Hadamard, J. (1892), "Essai sur l'étude des fonctions données par leur développement de Taylor", Journal de Mathématiques Pures et Appliquées, 4^e Série VIII . Also in Thèses présentées à la faculté des sciences de Paris pour obtenir le grade de docteur ès sciences mathématiques, Paris: Gauthier-Villars et fils, 1892.
↑ Lang, Serge (2002), Complex Analysis: Fourth Edition, Springer, pp. 55–56, ISBN 0-387-98592-1 Graduate Texts in Mathematics

External links

Weisstein, Eric W., "Cauchy-Hadamard theorem", MathWorld.