Categorical quotient
In algebraic geometry, given a category C, a categorical quotient of an object X with action of a group G is a morphism 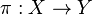 that
that
- (i) is invariant; i.e.,
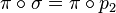 where
where 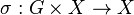 is the given group action and p2 is the projection.
is the given group action and p2 is the projection. - (ii) satisfies the universal property: any morphism
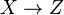 satisfying (i) uniquely factors through
satisfying (i) uniquely factors through 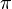 .
.
One of the main motivations for the development of geometric invariant theory was the construction of a categorical quotient for varieties or schemes.
Note 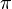 need not be surjective. Also, if it exists, a categorical quotient is unique up to a canonical isomorphism. In practice, one takes C to be the category of varieties or the category of schemes over a fixed scheme. A categorical quotient
need not be surjective. Also, if it exists, a categorical quotient is unique up to a canonical isomorphism. In practice, one takes C to be the category of varieties or the category of schemes over a fixed scheme. A categorical quotient 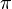 is a universal categorical quotient if it is stable under base change: for any
is a universal categorical quotient if it is stable under base change: for any 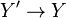 ,
, 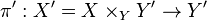 is a categorical quotient.
is a categorical quotient.
A basic result is that geometric quotients (e.g., 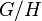 ) and GIT quotients (e.g.,
) and GIT quotients (e.g., 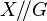 ) are categorical quotients.
) are categorical quotients.
References
- Mumford, David; Fogarty, J.; Kirwan, F. Geometric invariant theory. Third edition. Ergebnisse der Mathematik und ihrer Grenzgebiete (2) (Results in Mathematics and Related Areas (2)), 34. Springer-Verlag, Berlin, 1994. xiv+292 pp. MR 1304906 ISBN 3-540-56963-4