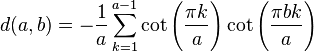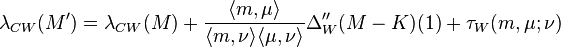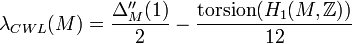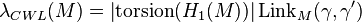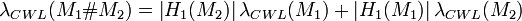Casson invariant
In 3-dimensional topology, a part of the mathematical field of geometric topology, the Casson invariant is an integer-valued invariant of oriented integral homology 3-spheres, introduced by Andrew Casson.
Kevin Walker (1992) found an extension to rational homology 3-spheres, called the Casson–Walker invariant, and Christine Lescop (1995) extended the invariant to all closed oriented 3-manifolds.
Definition
A Casson invariant is a surjective map λ from oriented integral homology 3-spheres to Z satisfying the following properties:
- λ(S3) = 0.
- Let Σ be an integral homology 3-sphere. Then for any knot K and for any integer n, the difference
- is independent of n. Here
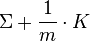 denotes
denotes  Dehn surgery on Σ by K.
Dehn surgery on Σ by K.
- For any boundary link K ∪ L in Σ the following expression is zero:
The Casson invariant is unique (with respect to the above properties) up to an overall multiplicative constant.
Properties
- If K is the trefoil then
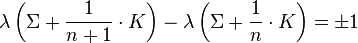 .
.
- The Casson invariant is 1 (or −1) for the Poincaré homology sphere.
- The Casson invariant changes sign if the orientation of M is reversed.
- The Rokhlin invariant of M is equal to the Casson invariant mod 2.
- The Casson invariant is additive with respect to connected summing of homology 3-spheres.
- The Casson invariant is a sort of Euler characteristic for Floer homology.
- For any integer n
- where
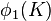 is the coefficient of
is the coefficient of 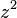 in the Alexander-Conway polynomial
in the Alexander-Conway polynomial 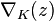 , and is congruent (mod 2) to the Arf invariant of K.
, and is congruent (mod 2) to the Arf invariant of K.
- The Casson invariant is the degree 1 part of the LMO invariant.
- The Casson invariant for the Seifert manifold
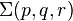 is given by the formula:
is given by the formula:
- where
The Casson invariant as a count of representations
Informally speaking, the Casson invariant counts half the number of conjugacy classes of representations of the fundamental group of a homology 3-sphere M into the group SU(2). This can be made precise as follows.
The representation space of a compact oriented 3-manifold M is defined as 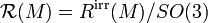 where
where 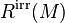 denotes the space of irreducible SU(2) representations of
denotes the space of irreducible SU(2) representations of 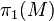 . For a Heegaard splitting
. For a Heegaard splitting 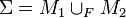 of
of 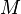 , the Casson invariant equals
, the Casson invariant equals 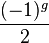 times the algebraic intersection of
times the algebraic intersection of 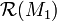 with
with 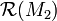 .
.
Generalizations
Rational homology 3-spheres
Kevin Walker found an extension of the Casson invariant to rational homology 3-spheres. A Casson-Walker invariant is a surjective map λCW from oriented rational homology 3-spheres to Q satisfying the following properties:
1. λ(S3) = 0.
2. For every 1-component Dehn surgery presentation (K, μ) of an oriented rational homology sphere M′ in an oriented rational homology sphere M:
where:
- m is an oriented meridian of a knot K and μ is the characteristic curve of the surgery.
- ν is a generator the kernel of the natural map H1(∂N(K), Z) → H1(M−K, Z).
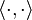 is the intersection form on the tubular neighbourhood of the knot, N(K).
is the intersection form on the tubular neighbourhood of the knot, N(K).- Δ is the Alexander polynomial normalized so that the action of t corresponds to an action of the generator of
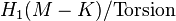 in the infinite cyclic cover of M−K, and is symmetric and evaluates to 1 at 1.
in the infinite cyclic cover of M−K, and is symmetric and evaluates to 1 at 1. 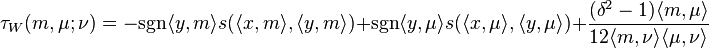
- where x, y are generators of H1(∂N(K), Z) such that
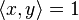 , v = δy for an integer δ and s(p, q) is the Dedekind sum.
, v = δy for an integer δ and s(p, q) is the Dedekind sum.
Note that for integer homology spheres, the Walker's normalization is twice that of Casson's: 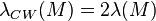 .
.
Compact oriented 3-manifolds
Christine Lescop defined an extension λCWL of the Casson-Walker invariant to oriented compact 3-manifolds. It is uniquely characterized by the following properties:
- If the first Betti number of M is zero,
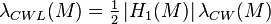 .
.
- If the first Betti number of M is one,
- where Δ is the Alexander polynomial normalized to be symmetric and take a positive value at 1.
- If the first Betti number of M is two,
- where γ is the oriented curve given by the intersection of two generators
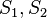 of
of 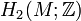 and
and 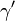 is the parallel curve to γ induced by the trivialization of the tubular neighbourhood of γ determined by
is the parallel curve to γ induced by the trivialization of the tubular neighbourhood of γ determined by 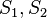 .
.
- If the first Betti number of M is three, then for a,b,c a basis for
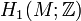 , then
, then
![\lambda_{CWL}(M)=\left\vert\mathrm{torsion}(H_1(M;\mathbb{Z}))\right\vert\left((a\cup b\cup c)([M])\right)^2](../I/m/b588bb147a2e8e726694ded334daa6f0.png) .
.
- If the first Betti number of M is greater than three,
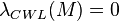 .
.
The Casson–Walker–Lescop invariant has the following properties:
- If the orientation of M, then if the first Betti number of M is odd the Casson–Walker–Lescop invariant is unchanged, otherwise it changes sign.
- For connect-sums of manifolds
SU(N)
In 1990, C. Taubes showed that the SU(2) Casson invarinat of a 3-homology shpere M has gauge theoretic interpretation as the Euler characteristic of 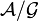 , where
, where 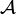 is the space of SU(2) connections on M and
is the space of SU(2) connections on M and 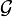 is the group of gauge transformations. He lead Chern–Simons invariant as a
is the group of gauge transformations. He lead Chern–Simons invariant as a 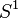 -valued Morse function on
-valued Morse function on 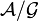 and pointed out that the SU(3) Casson invariant is important to make the invariants independent on perturbations. (Taubes (1990))
and pointed out that the SU(3) Casson invariant is important to make the invariants independent on perturbations. (Taubes (1990))
Boden and Herald (1998) defined an SU(3) Casson invariant.
References
- S. Akbulut and J. McCarthy, Casson's invariant for oriented homology 3-spheres— an exposition. Mathematical Notes, 36. Princeton University Press, Princeton, NJ, 1990. ISBN 0-691-08563-3
- M. Atiyah, New invariants of 3- and 4-dimensional manifolds. The mathematical heritage of Hermann Weyl (Durham, NC, 1987), 285–299, Proc. Sympos. Pure Math., 48, Amer. Math. Soc., Providence, RI, 1988.
- H. Boden and C. Herald, The SU(3) Casson invariant for integral homology 3-spheres. J. Differential Geom. 50 (1998), 147–206.
- C. Lescop, Global Surgery Formula for the Casson-Walker Invariant. 1995, ISBN 0-691-02132-5
- N. Saveliev, Lectures on the topology of 3-manifolds: An introduction to the Casson Invariant. de Gruyter, Berlin, 1999. ISBN 3-11-016271-7 ISBN 3-11-016272-5
- Taubes, Clifford Henry (1990), "Casson’s invariant and gauge theory.", J. Differential Geom. 31: 547–599
- K. Walker, An extension of Casson's invariant. Annals of Mathematics Studies, 126. Princeton University Press, Princeton, NJ, 1992. ISBN 0-691-08766-0 ISBN 0-691-02532-0
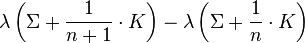
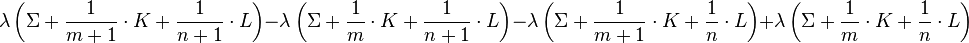
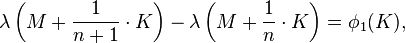
![\lambda(\Sigma(p,q,r))=-\frac{1}{8}\left[1-\frac{1}{3pqr}\left(1-p^2q^2r^2+p^2q^2+q^2r^2+p^2r^2\right)
-d(p,qr)-d(q,pr)-d(r,pq)\right]](../I/m/07abff868450267d6ad001c4efc07f83.png)