Cartan–Eilenberg resolution
In homological algebra, the Cartan–Eilenberg resolution is in a sense, a resolution of a complex. It can be used to construct hyper-derived functors.
Definition
Let 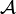 be an Abelian category with enough projectives, and let A∗ be a chain complex with objects in
be an Abelian category with enough projectives, and let A∗ be a chain complex with objects in 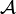 . Then a Cartan–Eilenberg resolution of A∗ is an upper half-plane double complex P∗∗ (i.e., Ppq = 0 for q < 0) consisting of projective objects of
. Then a Cartan–Eilenberg resolution of A∗ is an upper half-plane double complex P∗∗ (i.e., Ppq = 0 for q < 0) consisting of projective objects of 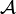 and a chain map ε : Pp0 → Ap such that
and a chain map ε : Pp0 → Ap such that
- Ap = 0 implies that the pth column is zero (Ppq = 0 for all q).
- For any fixed column,
- the kernels of each of the horizontal maps starting at that column (which themselves form a complex) are in fact exact,
- the same is true for the images of those maps, and
- the same is true for the homology of those maps.
(In fact, it would suffice to require it for the kernels and homology - the case of images follows from these.) In particular, since the kernels, cokernels, and homology will all be projective, they will give a projective resolution of the kernels, cokernels, and homology of the original complex A•
There is an analogous definition using injective resolutions and cochain complexes.
The existence of Cartan–Eilenberg resolutions can be proved via the horseshoe lemma.
Hyper-derived functors
Given a right exact functor 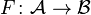 , one can define the left hyper-derived functors of F on a chain complex A∗ by constructing a Cartan–Eilenberg resolution ε : P∗∗ → A∗, applying F to P∗∗, and taking the homology of the resulting total complex.
, one can define the left hyper-derived functors of F on a chain complex A∗ by constructing a Cartan–Eilenberg resolution ε : P∗∗ → A∗, applying F to P∗∗, and taking the homology of the resulting total complex.
Similarly, one can also define right hyper-derived functors for left exact functors.
See also
References
- Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics 38, Cambridge University Press, ISBN 978-0-521-55987-4, MR 1269324