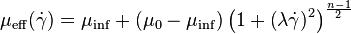Carreau fluid

Carreau fluid is a type of generalized Newtonian fluid where viscosity, 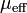$\mu_{\operatorname{eff}}$ , depends upon the shear rate, 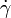$\dot \gamma$ , by the following equation:

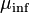\mu_{\operatorname{eff}}(\dot \gamma) = \mu_{\operatorname{\inf}} + (\mu_0 - \mu_{\operatorname{\inf}}) \left(1+\left(\lambda \dot \gamma\right) ^2 \right) ^ {\frac {n-1} {2}}

Where: $\mu_0$ , $\mu_{\operatorname{\inf}}$ , $\lambda$ and $n$ are material coefficients.

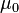$\mu_0$ = viscosity at zero shear rate (Pa.s)

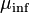$\mu_{\operatorname{\inf}}$ = viscosity at infinite shear rate (Pa.s)

$\lambda$ = relaxation time (s)

$n$ = power index

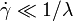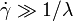At low shear rate ( $\dot \gamma \ll 1/\lambda$ ) Carreau fluid behaves as a Newtonian fluid and at high shear rate ( $\dot \gamma \gg 1/\lambda$ ) as a power-law fluid.

The model was first proposed by Pierre Carreau.

References

Kennedy, P. K., Flow Analysis of Injection Molds. New York. Hanser. ISBN 1-56990-181-3

Carreau fluid

See also

References

External links