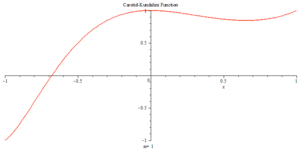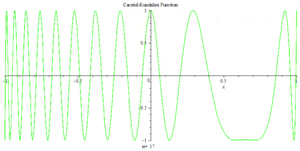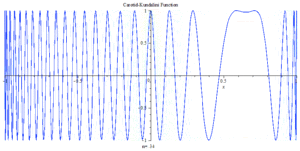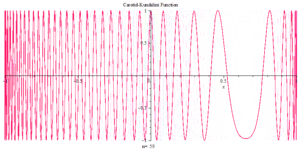
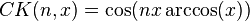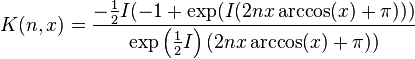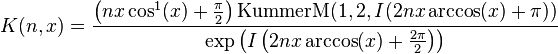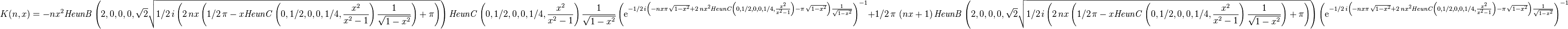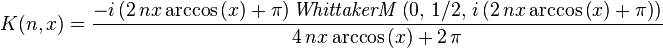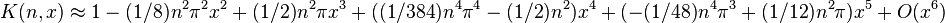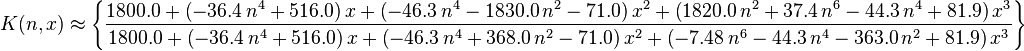Carotid–Kundalini function

Carotid–Kundalini function 2D animation with Maple
Carotid–Kundalini fractal land -1<x<0<br>Gaussian mountain -0.5<x<0.5<br>Oscillation land 0.5 <x
Carotid Kundalini function density plot with Maple
Carotid-Kundalini function derivative density plot
Carotid-Kundalini imaginary density plot
Carotid–Kundalini function phase diagram animation (Maple)
Carotid-Kundalini function derivative lace

The Carotid–Kundalini functionis closely associated with Carotid-Kundalini fractals coined by popular science columnist Clifford A. Pickover[1] and it is defined as follows[2]

CK(n,x)=\cos(nx\arccos(x))

Relations With Other Special Functions

K(n,x)=\frac{ -\frac 1 2 I(-1+\exp(I(2nx\arccos(x)+\pi)))}{\exp\left(\frac 1 2 I\right) (2nx\arccos(x)+\pi))}
K(n,x)= \frac{\left(nx\cos^1(x)+\frac \pi 2 \right)\operatorname{KummerM}(1,2,I(2nx\arccos(x)+\pi))}{\exp\left(I\left(2nx\arccos(x)+\frac{2\pi}2\right)\right)}
K(n,x)=-n{x}^{2}{\it HeunB} \left( 2,0,0,0,\sqrt {2}\sqrt {1/2\,i \left( 2\,n x \left( 1/2\,\pi -x{\it HeunC} \left( 0,1/2,0,0,1/4,{\frac {{x}^{2}}{ {x}^{2}-1}} \right) {\frac {1}{\sqrt {1-{x}^{2}}}} \right) +\pi \right) } \right) {\it HeunC} \left( 0,1/2,0,0,1/4,{\frac {{x}^{2}}{{ x}^{2}-1}} \right) {\frac {1}{\sqrt {1-{x}^{2}}}} \left( {{\rm e}^{-1/ 2\,i \left( -nx\pi \,\sqrt {1-{x}^{2}}+2\,n{x}^{2}{\it HeunC} \left( 0 ,1/2,0,0,1/4,{\frac {{x}^{2}}{{x}^{2}-1}} \right) -\pi \,\sqrt {1-{x}^ {2}} \right) {\frac {1}{\sqrt {1-{x}^{2}}}}}} \right) ^{-1}+1/2\,\pi \, \left( nx+1 \right) {\it HeunB} \left( 2,0,0,0,\sqrt {2}\sqrt {1/2 \,i \left( 2\,nx \left( 1/2\,\pi -x{\it HeunC} \left( 0,1/2,0,0,1/4,{ \frac {{x}^{2}}{{x}^{2}-1}} \right) {\frac {1}{\sqrt {1-{x}^{2}}}} \right) +\pi \right) } \right) \left( {{\rm e}^{-1/2\,i \left( -nx \pi \,\sqrt {1-{x}^{2}}+2\,n{x}^{2}{\it HeunC} \left( 0,1/2,0,0,1/4,{ \frac {{x}^{2}}{{x}^{2}-1}} \right) -\pi \,\sqrt {1-{x}^{2}} \right) { \frac {1}{\sqrt {1-{x}^{2}}}}}} \right) ^{-1}

Series Expansion

K(n,x) \approx {1-(1/8)n^2\pi^2 x^2+(1/2)n^2\pi x^3+((1/384) n^4 \pi^4-(1/2) n^2) x^4+(-(1/48) n^4 \pi^3+(1/12) n^2\pi) x^5+O(x^6)}

Pate Approximation

K(n,x) \approx \left\{ {\frac { 1800.0+ \left( - 36.4\,{n}^{4}+ 516.0 \right) x+ \left( - 46.3\,{n}^{4}- 1830.0\,{n}^{2}- 71.0 \right) {x}^{2}+ \left( 1820.0\,{n}^{2}+ 37.4\,{n}^{6}- 44.3\,{n}^{4}+ 81.9 \right) { x}^{3}}{ 1800.0+ \left( - 36.4\,{n}^{4}+ 516.0 \right) x+ \left( - 46.3\,{n}^{4}+ 368.0\,{n}^{2}- 71.0 \right) {x}^{2}+ \left( - 7.48\,{ n}^{6}- 44.3\,{n}^{4}- 363.0\,{n}^{2}+ 81.9 \right) {x}^{3}}} \right\}

External links

References

  1. ↑
  2. ↑ Weisstein, Eric W. "Carotid–Kundalini Function." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Carotid-KundaliniFunction.html