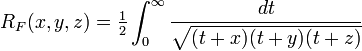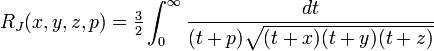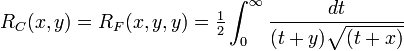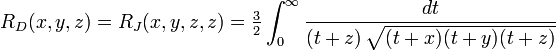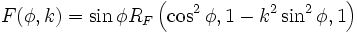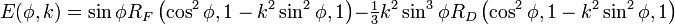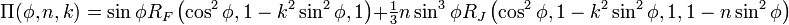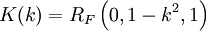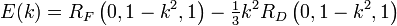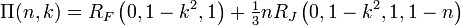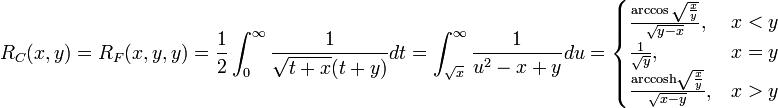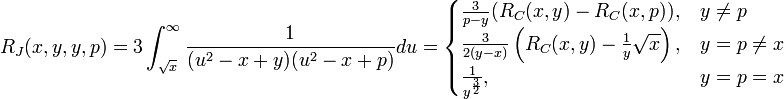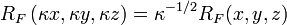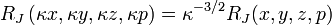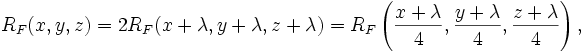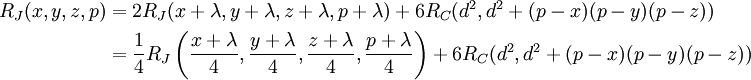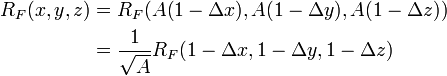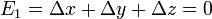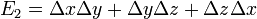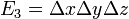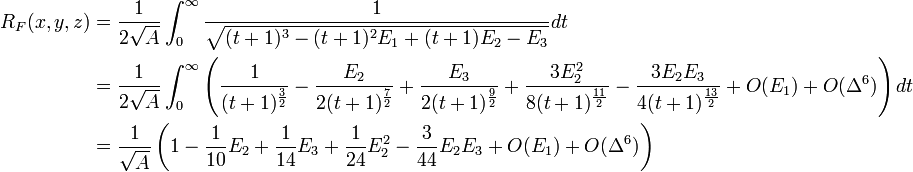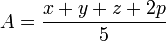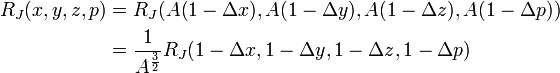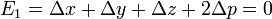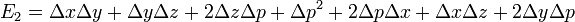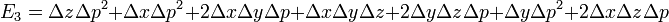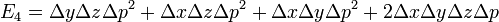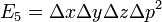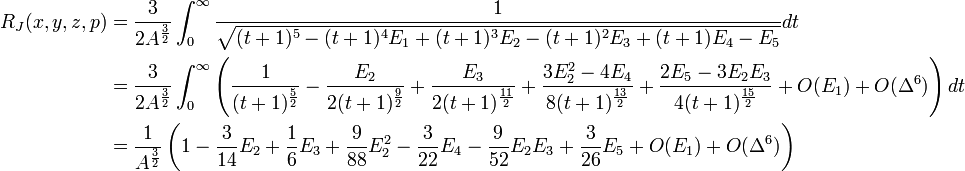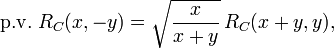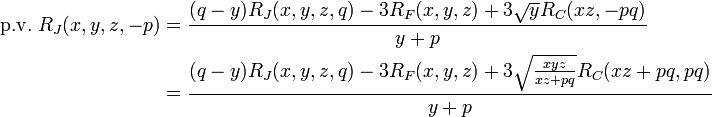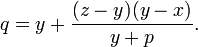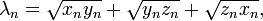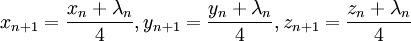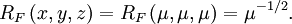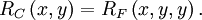Carlson symmetric form
In mathematics, the Carlson symmetric forms of elliptic integrals are a small canonical set of elliptic integrals to which all others may be reduced. They are a modern alternative to the Legendre forms. The Legendre forms may be expressed in terms of the Carlson forms and vice versa.
The Carlson elliptic integrals are:
Since 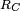 and
and 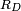 are special cases of
are special cases of 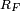 and
and 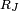 , all elliptic integrals can ultimately be evaluated in terms of just
, all elliptic integrals can ultimately be evaluated in terms of just 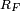 and
and 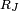 .
.
The term symmetric refers to the fact that in contrast to the Legendre forms, these functions are unchanged by the exchange of certain of their arguments. The value of 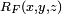 is the same for any permutation of its arguments, and the value of
is the same for any permutation of its arguments, and the value of 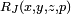 is the same for any permutation of its first three arguments.
is the same for any permutation of its first three arguments.
The Carlson elliptic integrals are named after Bille C. Carlson.
Relation to the Legendre forms
Incomplete elliptic integrals
Incomplete elliptic integrals can be calculated easily using Carlson symmetric forms:
(Note: the above are only valid for 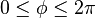 and
and 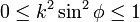 )
)
Complete elliptic integrals
Complete elliptic integrals can be calculated by substituting φ = 1⁄2π:
Special cases
When any two, or all three of the arguments of 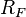 are the same, then a substitution of
are the same, then a substitution of 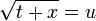 renders the integrand rational. The integral can then be expressed in terms of elementary transcendental functions.
renders the integrand rational. The integral can then be expressed in terms of elementary transcendental functions.
Similarly, when at least two of the first three arguments of 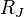 are the same,
are the same,
Properties
Homogeneity
By substituting in the integral definitions 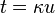 for any constant
for any constant 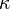 , it is found that
, it is found that
Duplication theorem
where 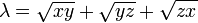 .
.
where 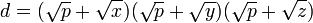 and
and 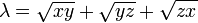
Series Expansion
In obtaining a Taylor series expansion for 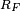 or
or 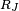 it proves convenient to expand about the mean value of the several arguments. So for
it proves convenient to expand about the mean value of the several arguments. So for 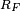 , letting the mean value of the arguments be
, letting the mean value of the arguments be 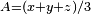 , and using homogeneity, define
, and using homogeneity, define 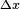 ,
, 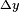 and
and 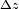 by
by
that is 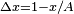 etc. The differences
etc. The differences 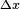 ,
, 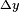 and
and 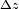 are defined with this sign (such that they are subtracted), in order to be in agreement with Carlson's papers. Since
are defined with this sign (such that they are subtracted), in order to be in agreement with Carlson's papers. Since 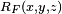 is symmetric under permutation of
is symmetric under permutation of  ,
,  and
and  , it is also symmetric in the quantities
, it is also symmetric in the quantities 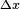 ,
, 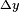 and
and 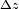 . It follows that both the integrand of
. It follows that both the integrand of 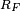 and its integral can be expressed as functions of the elementary symmetric polynomials in
and its integral can be expressed as functions of the elementary symmetric polynomials in 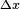 ,
, 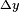 and
and 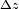 which are
which are
Expressing the integrand in terms of these polynomials, performing a multidimensional Taylor expansion and integrating term-by-term...
The advantage of expanding about the mean value of the arguments is now apparent; it reduces 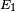 identically to zero, and so eliminates all terms involving
identically to zero, and so eliminates all terms involving 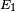 - which otherwise would be the most numerous.
- which otherwise would be the most numerous.
An ascending series for 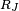 may be found in a similar way. There is a slight difficulty because
may be found in a similar way. There is a slight difficulty because 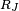 is not fully symmetric; its dependence on its fourth argument,
is not fully symmetric; its dependence on its fourth argument,  , is different from its dependence on
, is different from its dependence on  ,
,  and
and  . This is overcome by treating
. This is overcome by treating 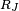 as a fully symmetric function of five arguments, two of which happen to have the same value
as a fully symmetric function of five arguments, two of which happen to have the same value  . The mean value of the arguments is therefore take to be
. The mean value of the arguments is therefore take to be
and the differences 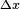 ,
, 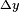
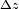 and
and 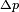 defined by
defined by
The elementary symmetric polynomials in 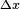 ,
, 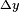 ,
, 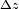 ,
, 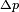 and (again)
and (again) 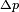 are in full
are in full
However, it is possible to simplify the formulae for 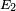 ,
, 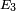 and
and 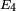 using the fact that
using the fact that 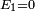 . Expressing the integrand in terms of these polynomials, performing a multidimensional Taylor expansion and integrating term-by-term as before...
. Expressing the integrand in terms of these polynomials, performing a multidimensional Taylor expansion and integrating term-by-term as before...
As with 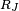 , by expanding about the mean value of the arguments, more than half the terms (those involving
, by expanding about the mean value of the arguments, more than half the terms (those involving 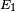 ) are eliminated.
) are eliminated.
Negative arguments
In general, the arguments x, y, z of Carlson's integrals may not be real and negative, as this would place a branch point on the path of integration, making the integral ambiguous. However, if the second argument of 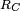 , or the fourth argument, p, of
, or the fourth argument, p, of 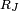 is negative, then this results in a simple pole on the path of integration. In these cases the Cauchy principal value (finite part) of the integrals may be of interest; these are
is negative, then this results in a simple pole on the path of integration. In these cases the Cauchy principal value (finite part) of the integrals may be of interest; these are
and
where
which must be greater than zero for 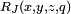 to be evaluated. This may be arranged by permuting x, y and z so that the value of y is between that of x and z.
to be evaluated. This may be arranged by permuting x, y and z so that the value of y is between that of x and z.
Numerical evaluation
The duplication theorem can be used for a fast and robust evaluation of the Carlson symmetric form of elliptic integrals
and therefore also for the evaluation of Legendre-form of elliptic integrals. Let us calculate 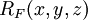 :
first, define
:
first, define 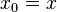 ,
, 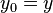 and
and 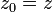 . Then iterate the series
. Then iterate the series
until the desired precision is reached: if 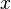 ,
, 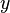 and
and 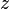 are non-negative, all of the series will converge quickly to a given value, say,
are non-negative, all of the series will converge quickly to a given value, say, 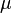 . Therefore,
. Therefore,
Note: for complex arguments and MATLAB use 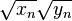 instead of
instead of 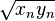 to get the correct values because of the complex square root branch choice ambiguity.
to get the correct values because of the complex square root branch choice ambiguity.
Evaluating 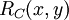 is much the same due to the relation
is much the same due to the relation
References and External links
- B. C. Carlson, John L. Gustafson 'Asymptotic approximations for symmetric elliptic integrals' 1993 arXiv
- B. C. Carlson 'Numerical Computation of Real Or Complex Elliptic Integrals' 1994 arXiv
- B. C. Carlson 'Elliptic Integrals:Symmetric Integrals' in Chap. 19 of Digital Library of Mathematical Functions. Release date 2010-05-07. National Institute of Standards and Technology.
- 'Profile: Bille C. Carlson' in Digital Library of Mathematical Functions. National Institute of Standards and Technology.
- Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), "Section 6.12. Elliptic Integrals and Jacobian Elliptic Functions", Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8