Capillary length

In fluid mechanics, capillary length is a characteristic length scale for an interface between two fluids which is subject both to gravitational acceleration and to a surface force due to surface tension in the interface.

The capillary length is defined as:^[1]

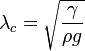\lambda_{c} = \sqrt{\frac{\gamma}{\rho g}}

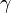where $g$ is the gravitational acceleration and $\rho$ is the density of the fluid, and $\gamma$ is the surface tension of the fluid-fluid interface.

For clean water and air at standard temperature and pressure, the capillary length is around 2 mm.

For a soap bubble in air, the capillary length is around 4 meters (13 feet).

A capillary surface that has a characteristic length smaller than the capillary length can be considered a low Bond number surface. A sessile drop whose largest dimension is smaller than the capillary length, for example, will take the shape of spherical cap, which is the solution to the Young-Laplace equation with gravity completely absent.

References

↑ G.K. Batchelor, 'An Introduction To Fluid Dynamics', Cambridge University Press (1967)

Capillary length

See also

References