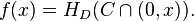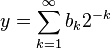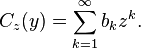Cantor function

In mathematics, the Cantor function is an example of a function that is continuous, but not absolutely continuous. It is also referred to as the Cantor ternary function, the Lebesgue function, Lebesgue's singular function, the Cantor-Vitali function, the Devil's staircase,[1] the Cantor staircase function,[2] and the Cantor-Lebesgue function.[3] Georg Cantor (1884) introduced the Cantor function and mentioned that Scheeffer pointed out that it was a counterexample to an extension of the fundamental theorem of calculus claimed by Harnack. The Cantor function was discussed and popularized by Scheeffer (1884), Lebesgue (1904) and Vitali (1905).
Definition
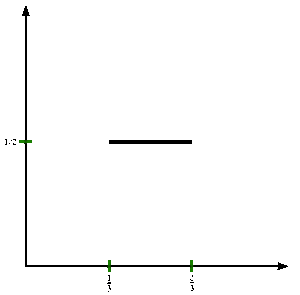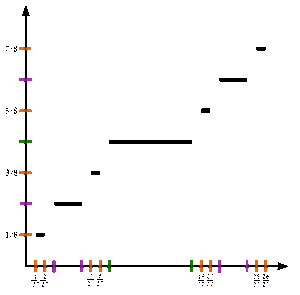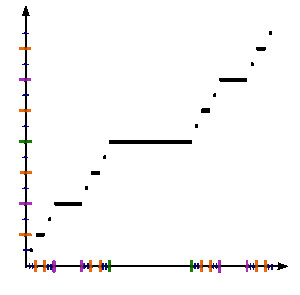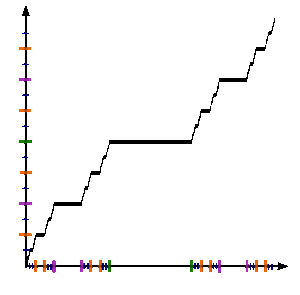
See figure. To formally define the Cantor function c : [0,1] → [0,1], let x be in [0,1] and obtain c(x) by the following steps:
- Express x in base 3.
- If x contains a 1, replace every digit after the first 1 by 0.
- Replace all 2s with 1s.
- Interpret the result as a binary number. The result is c(x).
For example:
- 1/4 becomes 0.02020202... base 3; there are no 1s so the next stage is still 0.02020202...; this is rewritten as 0.01010101...; when read in base 2, this is 1/3 so c(1/4) = 1/3.
- 1/5 becomes 0.01210121... base 3; the digits after the first 1 are replaced by 0s to produce 0.01000000...; this is not rewritten since there are no 2s; when read in base 2, this is 1/4 so c(1/5) = 1/4.
- 200/243 becomes 0.21102 (or 0.211012222...) base 3; the digits after the first 1 are replaced by 0s to produce 0.21; this is rewritten as 0.11; when read in base 2, this is 3/4 so c(200/243) = 3/4.
Properties
The Cantor function challenges naive intuitions about continuity and measure; though it is continuous everywhere and has zero derivative almost everywhere, c goes from 0 to 1 as x goes from 0 to 1, and takes on every value in between. The Cantor function is the most frequently cited example of a real function that is uniformly continuous (precisely, it is Hölder continuous of exponent α = log2/log3) but not absolutely continuous. It is constant on intervals of the form (0.x1x2x3...xn022222..., 0.x1x2x3...xn200000...), and every point not in the Cantor set is in one of these intervals, so its derivative is 0 outside of the Cantor set. On the other hand, it has no derivative at any point in an uncountable subset of the Cantor set containing the interval endpoints described above.
Extended to the left with value 0 and to the right with value 1, it is the cumulative probability distribution function of a random variable that is uniformly distributed on the Cantor set. This distribution, called the Cantor distribution, has no discrete part. That is, the corresponding measure is atomless. This is why there are no jump discontinuities in the function; any such jump would correspond to an atom in the measure.
However, no non-constant part of the Cantor function can be represented as an integral of a probability density function; integrating any putative probability density function that is not almost everywhere zero over any interval will give positive probability to some interval to which this distribution assigns probability zero. In particular, as Vitali (1905) pointed out, the function is not the integral of its derivative even though the derivative exists almost everywhere.
The Cantor function is the standard example of a singular function.
The Cantor function is non-decreasing, and so in particular its graph defines a rectifiable curve. Scheeffer (1884) showed that the arc length of its graph is 2.
Alternative definitions
Iterative construction

Below we define a sequence {ƒn} of functions on the unit interval that converges to the Cantor function.
Let ƒ0(x) = x.
Then, for every integer n ≥ 0, the next function ƒn+1(x) will be defined in terms of ƒn(x) as follows:
Let ƒn+1(x) = 0.5 × ƒn(3x), when 0 ≤ x ≤ 1/3 ;
Let ƒn+1(x) = 0.5, when 1/3 ≤ x ≤ 2/3 ;
Let ƒn+1(x) = 0.5 + 0.5 × ƒn(3 x − 2), when 2/3 ≤ x ≤ 1.
The three definitions are compatible at the end-points 1/3 and 2/3, because ƒn(0) = 0 and ƒn(1) = 1 for every n, by induction. One may check that ƒn converges pointwise to the Cantor function defined above. Furthermore, the convergence is uniform. Indeed, separating into three cases, according to the definition of ƒn+1, one sees that
If ƒ denotes the limit function, it follows that, for every n ≥ 0,
Also the choice of starting function does not really matter, provided ƒ0(0) = 0, ƒ0(1) = 1 and ƒ0 is bounded.
Fractal volume
The Cantor function is closely related to the Cantor set. The Cantor set C can be defined as the set of those numbers in the interval [0, 1] that do not contain the digit 1 in their base-3 (triadic) expansion, except if the 1 is followed by zeros only (in which case the tail 1000 can be replaced by 0222
can be replaced by 0222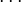 to get rid of any 1). It turns out that the Cantor set is a fractal with (uncountably) infinitely many points (zero-dimensional volume), but zero length (one-dimensional volume). Only the D-dimensional volume
to get rid of any 1). It turns out that the Cantor set is a fractal with (uncountably) infinitely many points (zero-dimensional volume), but zero length (one-dimensional volume). Only the D-dimensional volume 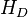 (in the sense of a Hausdorff-measure) takes a finite value, where
(in the sense of a Hausdorff-measure) takes a finite value, where 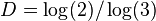 is the fractal dimension of C. We may define the Cantor function alternatively as the D-dimensional volume of sections of the Cantor set
is the fractal dimension of C. We may define the Cantor function alternatively as the D-dimensional volume of sections of the Cantor set
Generalizations
Let
be the dyadic (binary) expansion of the real number 0 ≤ y ≤ 1 in terms of binary digits bk = {0,1}. Then consider the function
For z = 1/3, the inverse of the function x = 2 C1/3(y) is the Cantor function. That is, y = y(x) is the Cantor function. In general, for any z < 1/2, Cz(y) looks like the Cantor function turned on its side, with the width of the steps getting wider as z approaches zero.
Minkowski's question mark function visually loosely resembles the Cantor function, having the general appearance of a "smoothed out" Cantor function, and can be constructed by passing from a continued fraction expansion to a binary expansion, just as the Cantor function can be constructed by passing from a ternary expansion to a binary expansion. The question mark function has the interesting property of having vanishing derivatives at all rational numbers.
Notes
- ↑ Thomson, Bruckner & Bruckner 2008, p. 252.
- ↑ http://mathworld.wolfram.com/CantorStaircaseFunction.html
- ↑ Bass 2013, p. 28.
References
- Bass, Richard Franklin (2013) [2011]. Real analysis for graduate students (Second ed.). Createspace Independent Publishing. ISBN 978-1-4818-6914-0.
- Cantor, G. (1884), "De la puissance des ensembles parfaits de points", Acta Math. 4: 381–392, doi:10.1007/BF02418423 Reprinted in: E. Zermelo (Ed.), Gesammelte Abhandlungen Mathematischen und Philosophischen Inhalts, Springer, New York, 1980.
- Darst, Richard B.; Palagallo, Judith A.; Price, Thomas E. (2010), Curious curves, Hackensack, NJ: World Scientific Publishing Co. Pte. Ltd., ISBN 978-981-4291-28-6, MR 2681574
- Dovgoshey, O.; Martio, O.; Ryazanov, V.; Vuorinen, M. (2006), "The Cantor function", Expo. Math. 24 (1): 1–37, MR 2195181
- Fleron, J.F. (1994), "A note on the history of the Cantor set and Cantor function", Math. Mag. 67: 136–140, JSTOR 2690689
- Lebesgue, H. (1904), Leçons sur l’intégration et la recherche des fonctions primitives, Paris: Gauthier-Villars
- Scheeffer, Ludwig (1884), "Allgemeine Untersuchungen über Rectification der Curven", Acta Math. 5: 49–82, doi:10.1007/BF02421552
- Thomson, Brian S.; Bruckner, Judith B.; Bruckner, Andrew M. (2008) [2001]. Elementary real analysis (Second ed.). ClassicalRealAnalysis.com. ISBN 978-1-4348-4367-8.
- Vitali, A. (1905), "Sulle funzioni integrali", Atti Accad. Sci. Torino Cl. Sci. Fis. Mat. Natur. 40: 1021–1034
![\max_{x \in [0, 1]} |f_{n+1}(x) - f_n(x)| \le \frac 1 2 \, \max_{x \in [0, 1]} |f_{n}(x) - f_{n-1}(x)|, \quad n \ge 1.](../I/m/f75c9533bc07b41b1f2f535d91eb201f.png)
![\max_{x \in [0, 1]} |f(x) - f_n(x)| \le 2^{-n+1} \, \max_{x \in [0, 1]} |f_1(x) - f_0(x)|.](../I/m/3481ae1999c4121cad39e62ca7a62b09.png)