Cantellated tesseractic honeycomb
| Cantellated tesseractic honeycomb | |
|---|---|
| (No image) | |
| Type | Uniform 4-honeycomb |
| Schläfli symbol | t0,2{4,3,3,4} |
| Coxeter-Dynkin diagram | |
| 4-face type | t0,2{4,3,3} t1{3,3,4} {3,4}×{} |
| Cell type | Octahedron Rhombicuboctahedron Triangular prism |
| Face type | {3}, {4} |
| Vertex figure | Cubic wedge |
| Coxeter group | 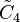 = [4,3,3,4] = [4,3,3,4]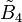 = [4,3,31,1] = [4,3,31,1] |
| Dual | |
| Properties | vertex-transitive |
In four-dimensional Euclidean geometry, the cantellated tesseractic honeycomb is a uniform space-filling tessellation (or honeycomb) in Euclidean 4-space. It is constructed by a cantellation of a tesseractic honeycomb creating cantellated tesseracts, and new 24-cell and octahedral prism facets at the original vertices.
Related honeycombs
The [4,3,3,4], ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , Coxeter group generates 31 permutations of uniform tessellations, 21 with distinct symmetry and 20 with distinct geometry. The expanded tesseractic honeycomb (also known as the stericated tesseractic honeycomb) is geometrically identical to the tesseractic honeycomb. Three of the symmetric honeycombs are shared in the [3,4,3,3] family. Two alternations (13) and (17), and the quarter tesseractic (2) are repeated in other families.
, Coxeter group generates 31 permutations of uniform tessellations, 21 with distinct symmetry and 20 with distinct geometry. The expanded tesseractic honeycomb (also known as the stericated tesseractic honeycomb) is geometrically identical to the tesseractic honeycomb. Three of the symmetric honeycombs are shared in the [3,4,3,3] family. Two alternations (13) and (17), and the quarter tesseractic (2) are repeated in other families.
| Extended symmetry |
Extended diagram |
Order | Honeycombs |
|---|---|---|---|
| [4,3,3,4]: | ×1 | ||
| [[4,3,3,4]] | ×2 | ||
| [(3,3)[1+,4,3,3,4,1+]] = [(3,3)[31,1,1,1]] = [3,4,3,3] |
= = |
×6 |
The [4,3,31,1], ![]()
![]()
![]()
![]()
![]()
![]()
![]() , Coxeter group generates 31 permutations of uniform tessellations, 23 with distinct symmetry and 4 with distinct geometry. There are two alternated forms: the alternations (19) and (24) have the same geometry as the 16-cell honeycomb and snub 24-cell honeycomb respectively.
, Coxeter group generates 31 permutations of uniform tessellations, 23 with distinct symmetry and 4 with distinct geometry. There are two alternated forms: the alternations (19) and (24) have the same geometry as the 16-cell honeycomb and snub 24-cell honeycomb respectively.
| Extended symmetry |
Extended diagram |
Order | Honeycombs |
|---|---|---|---|
| [4,3,31,1]: | ×1 | ||
| <[4,3,31,1]>: =[4,3,3,4] |
= |
×2 | |
| [3[1+,4,3,31,1]] = [3[3,31,1,1]] = [3,3,4,3] |
= = |
×3 | |
| [(3,3)[1+,4,3,31,1]] = [(3,3)[31,1,1,1]] = [3,4,3,3] |
= = |
×12 |
See also
Regular and uniform honeycombs in 4-space:
- Tesseractic honeycomb
- Demitesseractic honeycomb
- 24-cell honeycomb
- Truncated 24-cell honeycomb
- Snub 24-cell honeycomb
- 5-cell honeycomb
- Truncated 5-cell honeycomb
- Omnitruncated 5-cell honeycomb
Notes
References
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- George Olshevsky, Uniform Panoploid Tetracombs, Manuscript (2006) (Complete list of 11 convex uniform tilings, 28 convex uniform honeycombs, and 143 convex uniform tetracombs)
- Richard Klitzing, 4D, Euclidean tesselations#4D o3x3o *b3o4x, x4o3x3o4o - srittit - O90
- Conway JH, Sloane NJH (1998). Sphere Packings, Lattices and Groups (3rd ed.). ISBN 0-387-98585-9.
| Fundamental convex regular and uniform honeycombs in dimensions 2–10 | |||||
|---|---|---|---|---|---|
| Family | 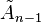 |
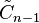 |
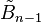 |
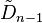 |
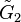 / / 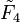 / /  |
| Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| Uniform 5-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| Uniform 6-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| Uniform 7-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| Uniform 8-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| Uniform 9-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| Uniform n-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |