Candidate key
In the relational model of databases, a candidate key of a relation is a minimal superkey for that relation; that is, a set of attributes such that:
- the relation does not have two distinct tuples (i.e. rows or records in common database language) with the same values for these attributes (which means that the set of attributes is a superkey)
- there is no proper subset of these attributes for which (1) holds (which means that the set is minimal).
The constituent attributes are called prime attributes. Conversely, an attribute that does not occur in ANY candidate key is called a non-prime attribute.
Since a relation contains no duplicate tuples, the set of all its attributes is a superkey if NULL values are not used. It follows that every relation will have at least one candidate key.
The candidate keys of a relation tell us all the possible ways we can identify its tuples. As such they are an important concept for the design of database schema.
Example
The definition of candidate keys can be illustrated with the following (abstract) example. Consider a relation variable (relvar) R with attributes (A, B, C, D) that has only the following two legal values r1 and r2:
| A | B | C | D |
|---|---|---|---|
| a1 | b1 | c1 | d1 |
| a1 | b2 | c2 | d1 |
| a2 | b1 | c2 | d1 |
| A | B | C | D |
|---|---|---|---|
| a1 | b1 | c1 | d1 |
| a1 | b2 | c2 | d1 |
| a1 | b1 | c2 | d2 |
Here r2 differs from r1 only in the A and D values of the last tuple.
For r1 the following sets have the uniqueness property, i.e., there are no two distinct tuples in the instance with the same values for the attributes in the set:
- {A,B}, {A,C}, {B,C}, {A,B,C}, {A,B,D}, {A,C,D}, {B,C,D}, {A,B,C,D}
For r2 the uniqueness property holds for the following sets;
- {B,C}, {B,D}, {C,D}, {A,B,C}, {A,B,D}, {A,C,D}, {B,C,D}, {A,B,C,D}
Since superkeys of a relvar are those sets of attributes that have the uniqueness property for all legal values of that relvar and because we assume that r1 and r2 are all the legal values that R can take, we can determine the set of superkeys of R by taking the intersection of the two lists:
- {B,C}, {A,B,C}, {A,B,D}, {A,C,D}, {B,C,D}, {A,B,C,D}
Finally we need to select those sets for which there is no proper subset in the list, which are in this case:
- {B,C}, {A,B,D}, {A,C,D}
These are indeed the candidate keys of relvar R.
We have to consider all the relations that might be assigned to a relvar to determine whether a certain set of attributes is a candidate key. For example, if we had considered only r1 then we would have concluded that {A,B} is a candidate key, which is incorrect. However, we might be able to conclude from such a relation that a certain set is not a candidate key, because that set does not have the uniqueness property (example {A,D} for r1). Note that the existence of a proper subset of a set that has the uniqueness property cannot in general be used as evidence that the superset is not a candidate key. In particular, note that in the case of an empty relation, every subset of the heading has the uniqueness property, including the empty set.
Determining candidate keys
The set of all candidate keys can be computed
e.g. from the set of functional dependencies.
To this end we need to define the attribute closure 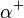 for an attribute set
for an attribute set  .
The set
.
The set 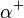 contains all attributes that are functionally implied by
contains all attributes that are functionally implied by  .
.
It is quite simple to find a single candidate key.
We start with a set  of attributes and try to remove successively each attribute.
If after removing an attribute the attribute closure stays the same,
then this attribute is not necessary and we can remove it permanently.
We call the result
of attributes and try to remove successively each attribute.
If after removing an attribute the attribute closure stays the same,
then this attribute is not necessary and we can remove it permanently.
We call the result 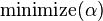 .
If
.
If  is the set of all attributes,
then
is the set of all attributes,
then 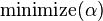 is a candidate key.
is a candidate key.
Actually we can detect every candidate key with this procedure
by simply trying every possible order of removing attributes.
However there are much more permutations of attributes (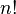 )
than subsets (
)
than subsets (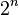 ).
That is, many attribute orders will lead to the same candidate key.
).
That is, many attribute orders will lead to the same candidate key.
There is a fundamental difficulty for efficient algorithms for candidate key computation:
Certain sets of functional dependencies lead to exponentially many candidate keys.
Consider the 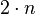 functional dependencies
functional dependencies
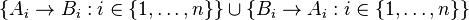 which yields
which yields 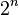 candidate keys:
candidate keys:
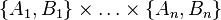 .
That is, the best we can expect is an algorithm that is efficient with respect to the number of candidate keys.
.
That is, the best we can expect is an algorithm that is efficient with respect to the number of candidate keys.
The following algorithm actually runs in polynomial time in the number of candidate keys and functional dependencies:[1]
K[0] := minimize(A); /* A is the set of all attribute */ n := 1; /* Number of Keys known so far */ i := 0; /* Currently processed key */ while i < n do foreach α → β ∈ F do S := α ∪ (K[i] − β); found := false; for j := 0 to n-1 do if K[j] ⊆ S then found := true; if not found then K[n] := minimize(S); n := n + 1;
The idea behind the algorithm is that given a candidate key 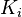 and a functional dependency
and a functional dependency  ,
the reverse application of the functional dependency yields
the set
,
the reverse application of the functional dependency yields
the set 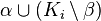 ,
which is a key, too.
It may however be covered by other already known candidate keys.
(The algorithm checks this case using the 'found' variable.)
If not, then minimizing the new key yields a new candidate key.
The key insight is (pun not intended) that all candidate keys can be created this way.
,
which is a key, too.
It may however be covered by other already known candidate keys.
(The algorithm checks this case using the 'found' variable.)
If not, then minimizing the new key yields a new candidate key.
The key insight is (pun not intended) that all candidate keys can be created this way.
See also
- Alternate key
- Compound key
- Database normalization
- Primary key
- Relational database
- Superkey
- Prime implicant is the corresponding notion of a candidate key in boolean logic
References
- ↑ L. Lucchesi, Cláudio; Osborn, Sylvia L. (October 1978). "Candidate keys for relations". Journal of Computer and System Sciences 17 (2): 270–279. doi:10.1016/0022-0000(78)90009-0.
- Date, Christopher (2003). "5: Integrity". An Introduction to Database Systems. Addison-Wesley. pp. 268–276. ISBN 978-0-321-18956-1.
External links
- Relational Database Management Systems - Database Design - Terms of Reference - Keys: An overview of the different types of keys in the RDBMS (Relational Database Management System).
| ||||||||||||||||||||||||||