Callan–Symanzik equation

In physics, the Callan–Symanzik equation is a differential equation describing the evolution of the n-point correlation functions under variation of the energy scale at which the theory is defined and involves the beta-function of the theory and the anomalous dimensions. This equation has the following structure

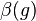\left[M\frac{\partial }{\partial M}+\beta(g)\frac{\partial }{\partial g}+n\gamma\right] G^{(n)}(x_1,x_2,\ldots,x_n;M,g)=0

being \beta(g) the beta function and 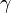\gamma the scaling of the fields.

In quantum electrodynamics this equation takes the form

\left[M\frac{\partial }{\partial M}+\beta(e)\frac{\partial }{\partial e}+n\gamma_2 +m\gamma_3\right]G^{(n,m)}(x_1,x_2,\ldots,x_n;M,e)=0

being n and m the number of electrons and photons respectively.

It was discovered independently by Curtis Callan[1] and Kurt Symanzik[2][3] in 1970. Later it was used to understand asymptotic freedom.

This equation arises in the framework of renormalization group. It is possible to treat the equation using perturbation theory.

See also

Notes

  1. ↑ C. G. Callan, Jr., Broken Scale Invariance in Scalar Field Theory, Phys. Rev. D 2, 1541–1547 (1970). APS
  2. ↑ K. Symanzik, Small Distance Behaviour in Field Theory and Power Counting, Commun. math. Phys. 18, 227 (1970). SpringerLink
  3. ↑ K. Symanzik, Small-Distance-Behaviour Analysis and Wilson Expansions, Commun. math. Phys. 23, 49 (1971). SpringerLink

References