C-minimal theory

In model theory, a branch of mathematical logic, a C-minimal theory is a theory that is "minimal" with respect to a ternary relation C with certain properties. Algebraically closed fields with a (Krull) valuation are perhaps the most important example.

This notion was defined in analogy to the o-minimal theories, which are "minimal" (in the same sense) with respect to a linear order.

Definition

A C-relation is a ternary relation C(x;yz) that satisfies the following axioms.

$\forall xyz\, [ C(x;yz)\rightarrow C(x;zy) ],$
$\forall xyz\, [ C(x;yz)\rightarrow\neg C(y;xz) ],$
$\forall xyzw\, [ C(x;yz)\rightarrow (C(w;yz)\vee C(x;wz)) ],$
$\forall xy\, [ x\neq y \rightarrow \exists z\neq y\, C(x;yz) ].$

A C-minimal structure is a structure M, in a signature containing the symbol C, such that C satisfies the above axioms and every set of elements of M that is definable with parameters in M is a Boolean combination of instances of C, i.e. of formulas of the form C(x;bc), where b and c are elements of M.

A theory is called C-minimal if all of its models are C-minimal. A structure is called strongly C-minimal if its theory is C-minimal. One can construct C-minimal structures which are not strongly C-minimal.

Example

For a prime number p and a p-adic number a let |a|_p denote its p-adic norm. Then the relation defined by 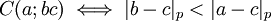$C(a;bc) \iff |b-c|_p < |a-c|_p$ is a C-relation, and the theory of Q_p with addition and this relation is C-minimal. The theory of Q_p as a field, however, is not C-minimal.

References

Macpherson, Dugald; Steinhorn, Charles (1996), "On variants of o-minimality", Annals of Pure and Applied Logic 79 (2): 165–209, doi:10.1016/0168-0072(95)00037-2
Haskell, Deirdre; Macpherson, Dugald (1994), "Cell decompositions of C-minimal structures", Annals of Pure and Applied Logic 66 (2): 113–162, doi:10.1016/0168-0072(94)90064-7