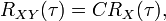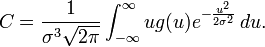Bussgang theorem

In mathematics, the Bussgang theorem is a theorem of stochastic analysis. The theorem states that the crosscorrelation of a Gaussian signal before and after it has passed through a nonlinear operation are equal up to a constant. It was first published by Julian J. Bussgang in 1952 while he was at the Massachusetts Institute of Technology.[1]

Statement of the theorem

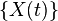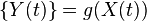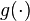Let \left\{X(t)\right\} be a zero-mean stationary Gaussian random process and \left \{ Y(t) \right\} = g(X(t)) where g(\cdot) is a nonlinear amplitude distortion.

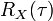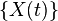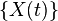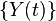If R_X(\tau) is the autocorrelation function of \left\{ X(t) \right\}, then the cross-correlation function of \left\{ X(t) \right\} and \left\{ Y(t) \right\} is

R_{XY}(\tau) = CR_X(\tau),

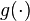where C is a constant that depends only on g(\cdot) .

It can be further shown that

C = \frac{1}{\sigma^3\sqrt{2\pi}}\int_{-\infty}^\infty ug(u)e^{-\frac{u^2}{2\sigma^2}} \, du.

Application

This theorem implies that a simplified correlator can be designed. Instead of having to multiply two signals, the cross-correlation problem reduces to the gating of one signal with another.

References

  1. ↑ J.J. Bussgang,"Cross-correlation function of amplitude-distorted Gaussian signals", Res. Lab. Elec., Mas. Inst. Technol., Cambridge MA, Tech. Rep. 216, March 1952.

Further reading