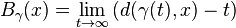Busemann function

Busemann functions were introduced by Busemann to study the large-scale geometry of metric spaces in his seminal The Geometry of Geodesics.^[1] More recently, Busemann functions have been used by probabilists to study asymptotic properties in models of first-passage percolation.^[2]^[3]

Definition

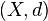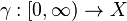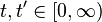Let $(X,d)$ be a metric space. A ray is a path $\gamma : [0,\infty) \to X$ which minimizes distance everywhere along its length. i.e., for all $t,t' \in [0,\infty)$ ,

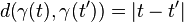d\big(\gamma(t), \gamma(t') \big) = \big| t - t' \big|

Equivalently, a ray is an isometry from the "canonical ray" (the set 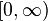$[0,\infty)$ equipped with the Euclidean metric) into the metric space X.

Given a ray γ, the Busemann function 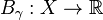$B_\gamma : X \to \mathbb R$ is defined by

B_\gamma(x)=\lim_{t\to\infty}\big( d\big( \gamma(t), x \big) - t \big)

That is, when t is very large, the distance 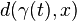$d\big( \gamma(t), x \big)$ is approximately equal to 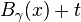$B_\gamma(x) + t$ . Given a ray γ, its Busemann function is always well-defined.

Loosely speaking, a Busemann function can be thought of as a "distance to infinity" along the ray γ.

References

↑ Busemann, Herbert. The geometry of geodesics. Vol. 6. DoverPublications. com, 1985.
↑ Hoffman, Christopher. "Coexistence for Richardson type competing spatial growth models." The Annals of Applied Probability 15.1B (2005): 739-747.
↑ Damron, Michael, and Jack Hanson. "Busemann functions and infinite geodesics in two-dimensional first-passage percolation." arXiv preprint arXiv:1209.3036 (2012).