Buckley–Leverett equation

In fluid dynamics, the Buckley–Leverett equation is a conservation equation used to model two-phase flow in porous media.^[1] The Buckley–Leverett equation or the Buckley–Leverett displacement can be interpreted as a way of incorporating the microscopic effects due to capillary pressure in two-phase flow into Darcy's law.

In a 1D sample (control volume), let $S(x,t)$ be the water saturation, then the Buckley–Leverett equation is

\frac{\partial S}{\partial t} = U(S)\frac{\partial S}{\partial x}

where

U(S) = \frac{Q}{\phi A} \frac{\mathrm{d} f}{\mathrm{d} S}.

$f$ is the fractional flow rate, $Q$ is the total flow, $\phi$ is porosity and $A$ is area of the cross-section in the sample volume.

Assumptions for validity

The Buckley–Leverett equation is derived for a 1D sample given

mass conservation
capillary pressure $p_c(S)$ is a function of water saturation $S$ only
$\mathrm{d}p_c/\mathrm{d}S = 0$ causing the pressure gradients of the two phases to be equal.
Flow is Linear
Flow is Steady-State
Formation is one Layer

General solution

The solution of the Buckley–Leverett equation has the form 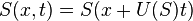$S(x,t) = S(x+U(S)t)$ which means that 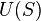$U(S)$ is the front velocity of the fluids at saturation $S$ .

References

↑ S.E. Buckley and M.C. Leverett (1942). "Mechanism of fluid displacements in sands". Transactions of the AIME (146): 107–116.

Buckley–Leverett equation

Assumptions for validity

General solution

See also

References