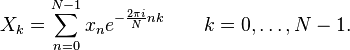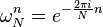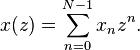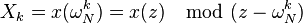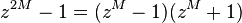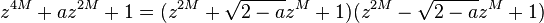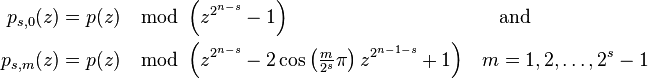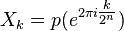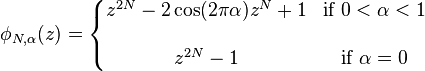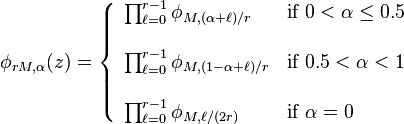Bruun's FFT algorithm

Bruun's algorithm is a fast Fourier transform (FFT) algorithm based on an unusual recursive polynomial-factorization approach, proposed for powers of two by G. Bruun in 1978 and generalized to arbitrary even composite sizes by H. Murakami in 1996. Because its operations involve only real coefficients until the last computation stage, it was initially proposed as a way to efficiently compute the discrete Fourier transform (DFT) of real data. Bruun's algorithm has not seen widespread use, however, as approaches based on the ordinary Cooley–Tukey FFT algorithm have been successfully adapted to real data with at least as much efficiency. Furthermore, there is evidence that Bruun's algorithm may be intrinsically less accurate than Cooley–Tukey in the face of finite numerical precision (Storn, 1993).

Nevertheless, Bruun's algorithm illustrates an alternative algorithmic framework that can express both itself and the Cooley–Tukey algorithm, and thus provides an interesting perspective on FFTs that permits mixtures of the two algorithms and other generalizations.

A polynomial approach to the DFT

Recall that the DFT is defined by the formula:

X_k = \sum_{n=0}^{N-1} x_n e^{-\frac{2\pi i}{N} nk } \qquad k = 0,\dots,N-1.

For convenience, let us denote the N roots of unity by ω_Nⁿ (n = 0, ..., N − 1):

\omega_N^n = e^{-\frac{2\pi i}{N} n }

and define the polynomial x(z) whose coefficients are x_n:

x(z) = \sum_{n=0}^{N-1} x_n z^n.

The DFT can then be understood as a reduction of this polynomial; that is, X_k is given by:

X_k = x(\omega_N^k) = x(z) \mod (z - \omega_N^k)

where mod denotes the polynomial remainder operation. The key to fast algorithms like Bruun's or Cooley–Tukey comes from the fact that one can perform this set of N remainder operations in recursive stages.

Recursive factorizations and FFTs

In order to compute the DFT, we need to evaluate the remainder of 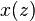$x(z)$ modulo N degree-1 polynomials as described above. Evaluating these remainders one by one is equivalent to the evaluating the usual DFT formula directly, and requires O(N²) operations. 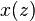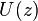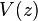However, one can combine these remainders recursively to reduce the cost, using the following trick: if we want to evaluate $x(z)$ modulo two polynomials $U(z)$ and $V(z)$ , we can first take the remainder modulo their product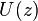 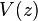$U(z)$ $V(z)$ , which reduces the degree of the polynomial 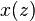$x(z)$ and makes subsequent modulo operations less computationally expensive.

The product of all of the monomials 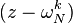$(z - \omega_N^k)$ for k=0..N-1 is simply 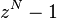$z^N-1$ (whose roots are clearly the N roots of unity). One then wishes to find a recursive factorization of 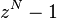$z^N-1$ into polynomials of few terms and smaller and smaller degree. To compute the DFT, one takes 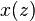$x(z)$ modulo each level of this factorization in turn, recursively, until one arrives at the monomials and the final result. If each level of the factorization splits every polynomial into an O(1) (constant-bounded) number of smaller polynomials, each with an O(1) number of nonzero coefficients, then the modulo operations for that level take O(N) time; since there will be a logarithmic number of levels, the overall complexity is O (N log N).

More explicitly, suppose for example that 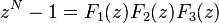$z^N-1 = F_1(z) F_2(z) F_3(z)$ , and that 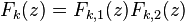$F_k(z) = F_{k,1}(z) F_{k,2}(z)$ , and so on. The corresponding FFT algorithm would consist of first computing x_k(z) = x(z) mod F_k(z), then computing x_k,j(z) = x_k(z) mod F_k,j(z), and so on, recursively creating more and more remainder polynomials of smaller and smaller degree until one arrives at the final degree-0 results.

Moreover, as long as the polynomial factors at each stage are relatively prime (which for polynomials means that they have no common roots), one can construct a dual algorithm by reversing the process with the Chinese Remainder Theorem.

Cooley–Tukey as polynomial factorization

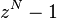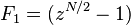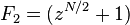The standard decimation-in-frequency (DIF) radix-r Cooley–Tukey algorithm corresponds closely to a recursive factorization. For example, radix-2 DIF Cooley–Tukey factors $z^N-1$ into $F_1 = (z^{N/2}-1)$ and $F_2 = (z^{N/2}+1)$ . These modulo operations reduce the degree of 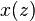$x(z)$ by 2, which corresponds to dividing the problem size by 2. Instead of recursively factorizing 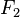$F_2$ directly, though, Cooley–Tukey instead first computes x₂(z ω_N), shifting all the roots (by a twiddle factor) so that it can apply the recursive factorization of 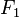$F_1$ to both subproblems. That is, Cooley–Tukey ensures that all subproblems are also DFTs, whereas this is not generally true for an arbitrary recursive factorization (such as Bruun's, below).

The Bruun factorization

The basic Bruun algorithm for powers of two N=2ⁿ factorizes z^2ⁿ-1 recursively via the rules:

z^{2M}-1 = (z^M - 1) (z^M + 1) \,

z^{4M} + az^{2M} + 1 = (z^{2M} + \sqrt{2-a}z^M+1) (z^{2M} - \sqrt{2-a}z^M + 1)

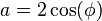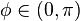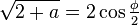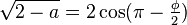where a is a real constant with |a| ≤ 2. If $a=2\cos(\phi)$ , $\phi\in(0,\pi)$ , then $\sqrt{2+a}=2\cos\tfrac\phi2$ and $\sqrt{2-a}=2\cos(\pi-\tfrac\phi2)$ .

At stage s, s=0,1,2,n-1, the intermediate state consists of 2^s polynomials 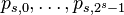$p_{s,0},\dots,p_{s,2^s-1}$ of degree 2^n-s - 1 or less , where

\begin{align} p_{s,0}(z)&= p(z) \mod \left(z^{2^{n-s}}-1\right)&\quad&\text{and}\\ p_{s,m}(z) &= p(z)\mod \left(z^{2^{n-s}}-2\cos\left(\tfrac{m}{2^s}\pi\right)z^{2^{n-1-s}}+1\right)&m&=1,2,\dots,2^s-1 \end{align}

By the construction of the factorization of z^2ⁿ-1, the polynomials p_s,m(z) each encode 2^n-s values

X_k=p(e^{2\pi i\tfrac{k}{2^n}})

of the Fourier transform, for m=0, the covered indices are k=0, 2^k, 2∙2^s, 3∙2^s,…, (2^n-s-1)∙2^s, for m>0 the covered indices are k=m, 2^s+1-m, 2^s+1+m, 2∙2^s+1-m, 2∙2^s+1+m, …, 2ⁿ-m.

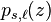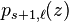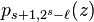During the transition to the next stage, the polynomial $p_{s,\ell}(z)$ is reduced to the polynomials $p_{s+1,\ell}(z)$ and $p_{s+1,2^s-\ell}(z)$ via polynomial division. If one wants to keep the polynomials in increasing index order, this pattern requires an implementation with two arrays. An implementation in place produces a predictable, but highly unordered sequence of indices, for example for N=16 the final order of the 8 linear remainders is (0, 4, 2, 6, 1, 7, 3, 5).

At the end of the recursion, for s=n-1, there remain 2^n-1 linear polynomials encoding two Fourier coefficients X₀ and X_2^n-1 for the first and for the any other kth polynomial the coefficients X_k and X_2ⁿ-k.

At each recursive stage, all of the polynomials of the common degree 4M-1 are reduced to two parts of half the degree 2M-1. The divisor of this polynomial remainder computation is a quadratic polynomial z^m, so that all reductions can be reduced to polynomial divisions of cubic by quadratic polynomials. There are N/2=2^n-1 of these small divisions at each stage, leading to an O (N log N) algorithm for the FFT.

Moreover, since all of these polynomials have purely real coefficients (until the very last stage), they automatically exploit the special case where the inputs x_n are purely real to save roughly a factor of two in computation and storage. One can also take straightforward advantage of the case of real-symmetric data for computing the discrete cosine transform (Chen and Sorensen, 1992).

Generalization to arbitrary radices

The Bruun factorization, and thus the Bruun FFT algorithm, was generalized to handle arbitrary even composite lengths, i.e. dividing the polynomial degree by an arbitrary radix (factor), as follows. First, we define a set of polynomials φ_N,α(z) for positive integers N and for α in [0,1) by:

\phi_{N, \alpha}(z) = \left\{ \begin{matrix} z^{2N} - 2 \cos (2 \pi \alpha) z^N + 1 & \mbox{if } 0 < \alpha < 1 \\ \\ z^{2N} - 1 & \mbox{if } \alpha = 0 \end{matrix} \right.

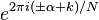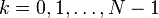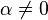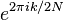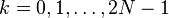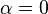Note that all of the polynomials that appear in the Bruun factorization above can be written in this form. The zeroes of these polynomials are $e^{2\pi i ( \pm\alpha + k ) / N}$ for $k=0,1,\dots,N-1$ in the $\alpha \neq 0$ case, and $e^{2\pi i k / 2N}$ for $k=0,1,\dots,2N-1$ in the $\alpha=0$ case. Hence these polynomials can be recursively factorized for a factor (radix) r via:

\phi_{rM, \alpha}(z) = \left\{ \begin{array}{ll} \prod_{\ell=0}^{r-1} \phi_{M,(\alpha+\ell)/r} & \mbox{if } 0 < \alpha \leq 0.5 \\ \\ \prod_{\ell=0}^{r-1} \phi_{M,(1-\alpha+\ell)/r} & \mbox{if } 0.5 < \alpha < 1 \\ \\ \prod_{\ell=0}^{r-1} \phi_{M,\ell/(2r)} & \mbox{if } \alpha = 0 \end{array} \right.

References

Georg Bruun, "z-Transform DFT filters and FFTs," IEEE Trans. on Acoustics, Speech and Signal Processing (ASSP) 26 (1), 56-63 (1978).
H. J. Nussbaumer, Fast Fourier Transform and Convolution Algorithms (Springer-Verlag: Berlin, 1990).
Yuhang Wu, "New FFT structures based on the Bruun algorithm," IEEE Trans. ASSP 38 (1), 188-191 (1990)
Jianping Chen and Henrik Sorensen, "An efficient FFT algorithm for real-symmetric data," Proc. ICASSP 5, 17-20 (1992).
Rainer Storn, "Some results in fixed point error analysis of the Bruun-FTT [sic] algorithm," IEEE Trans. Signal Processing 41 (7), 2371-2375 (1993).
Hideo Murakami, "Real-valued decimation-in-time and decimation-in-frequency algorithms," IEEE Trans. Circuits Syst. II: Analog and Digital Sig. Proc. 41 (12), 808-816 (1994).
Hideo Murakami, "Real-valued fast discrete Fourier transform and cyclic convolution algorithms of highly composite even length," Proc. ICASSP 3, 1311-1314 (1996).
Shashank Mittal, Md. Zafar Ali Khan, M. B. Srinivas, "A Comparative Study of Different FFT Architectures for Software Defined Radio", Lecture Notes in Computer Science 4599 (Embedded Computer Systems: Architectures, Modeling, and Simulation), 375-384 (2007). Proc. 7th Intl. Workshop, SAMOS 2007 (Samos, Greece, July 16–19, 2007).