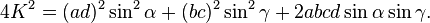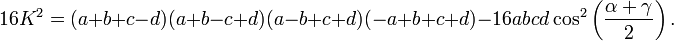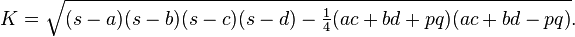Bretschneider's formula

A quadrilateral.

In geometry, Bretschneider's formula is the following expression for the area of a general convex quadrilateral:

K = \sqrt {(s-a)(s-b)(s-c)(s-d) - abcd \cdot \cos^2 \left(\frac{\alpha + \gamma}{2}\right)}
= \sqrt{(s-a)(s-b)(s-c)(s-d) - \tfrac{1}{2} abcd [ 1 + \cos (\alpha+ \gamma) ]} .

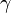Here, a, b, c, d are the sides of the quadrilateral, s is the semiperimeter, and \alpha \, and \gamma \, are two opposite angles.

Bretschneider's formula works on any convex quadrilateral, whether it is cyclic or not.

The German mathematician Carl Anton Bretschneider discovered the formula in 1842. The formula was also derived in the same year by the German mathematician Karl Georg Christian von Staudt.

Proof of Bretschneider's formula

Denote the area of the quadrilateral by K. Then we have

\begin{align} K &= \text{area of } \triangle ADB + \text{area of } \triangle BDC \\ &= \frac{a d \sin \alpha}{2} + \frac{b c \sin \gamma}{2}. \end{align}

Therefore

4K^2 = (ad)^2 \sin^2 \alpha + (bc)^2 \sin^2 \gamma + 2abcd \sin \alpha \sin \gamma. \,

The Law of Cosines implies that

a^2 + d^2 -2ad \cos \alpha = b^2 + c^2 -2bc \cos \gamma, \,

because both sides equal the square of the length of the diagonal BD. This can be rewritten as

\frac{(a^2 + d^2 - b^2 - c^2)^2}{4} = (ad)^2 \cos^2 \alpha +(bc)^2 \cos^2 \gamma -2 abcd \cos \alpha \cos \gamma. \,

Adding this to the above formula for 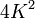4K^2 yields

\begin{align} 4K^2 + \frac{(a^2 + d^2 - b^2 - c^2)^2}{4} &= (ad)^2 + (bc)^2 - 2abcd \cos (\alpha + \gamma) \\ &= (ad + bc)^2 - 4abcd \cos^2 \left(\frac{\alpha + \gamma}{2}\right). \end{align}

Following the same steps as in Brahmagupta's formula, this can be written as

16K^2 = (a+b+c-d)(a+b-c+d)(a-b+c+d)(-a+b+c+d) - 16abcd \cos^2 \left(\frac{\alpha + \gamma}{2}\right).

Introducing the semiperimeter

s = \frac{a+b+c+d}{2},

the above becomes

16K^2 = 16(s-a)(s-b)(s-c)(s-d) - 16abcd \cos^2 \left(\frac{\alpha + \gamma}{2}\right)

and Bretschneider's formula follows.

Related formulas

Bretschneider's formula generalizes Brahmagupta's formula for the area of a cyclic quadrilateral, which in turn generalizes Heron's formula for the area of a triangle.

The trigonometric adjustment in Bretschneider's formula for non-cyclicality of the quadrilateral can be rewritten non-trigonometrically in terms of the sides and the diagonals p and q to give[1]

K = \sqrt{(s-a)(s-b)(s-c)(s-d) - \tfrac{1}{4}(ac+bd+pq)(ac+bd-pq)}.

References

  1. ↑ J. L. Coolidge, "A historically interesting formula for the area of a quadrilateral", American Mathematical Monthly, 46 (1939) 345–347.

External links