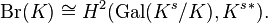Brauer group

In mathematics, the Brauer group of a field K is an abelian group whose elements are Morita equivalence classes of central simple algebras of finite rank over K and addition is induced by the tensor product of algebras. It arose out of attempts to classify division algebras over a field and is named after the algebraist Richard Brauer. The group may also be defined in terms of Galois cohomology. More generally, the Brauer group of a scheme is defined in terms of Azumaya algebras.

Construction

A central simple algebra (CSA) over a field K is a finite-dimensional associative K-algebra A, which is a simple ring, and for which the center is exactly K. Note that CSAs are in general not division algebras, though CSAs can be used to classify division algebras.

For example, the complex numbers C form a CSA over themselves, but not over R (the center is C itself, hence too large to be CSA over R). The finite-dimensional division algebras with center R (that means the dimension over R is finite) are the real numbers and the quaternions by a theorem of Frobenius, while any matrix ring over the reals or quaternions – M(n,R) or M(n,H) – is a CSA over the reals, but not a division algebra (if 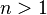$n > 1$ ).

We obtain an equivalence relation on CSAs over K by the Artin–Wedderburn theorem (Wedderburn's part, in fact), to express any CSA as a M(n,D) for some division algebra D. If we look just at D, that is, if we impose an equivalence relation identifying M(m,D) with M(n,D) for all integers m and n at least 1, we get the Brauer equivalence and the Brauer classes.

Given central simple algebras A and B, one can look at the their tensor product A ⊗ B as a K-algebra (see tensor product of R-algebras). It turns out that this is always central simple. A slick way to see this is to use a characterisation: a central simple algebra over K is a K-algebra that becomes a matrix ring when we extend the field of scalars to an algebraic closure of K.

Given this closure property for CSAs, they form a monoid under tensor product, compatible with Brauer equivalence, and the Brauer classes are all invertible: the inverse class to that of an algebra A is the one containing the opposite algebra A^op (the opposite ring with the same action by K since the image of K → A is in the center of A). In other words, for a CSA A we have A ⊗ A^op = M(n²,K), where n is the degree of A over K. (This provides a substantial reason for caring about the notion of an opposite algebra: it provides the inverse in the Brauer group.)

Examples

In the following cases, every finite-dimensional central division algebra over a field K is K itself, so that the Brauer group Br(K) is trivial:

- K is an algebraically closed field:^[1] more generally, this is true for any pseudo algebraically closed field^[2] or quasi-algebraically closed field.^[3]

- K is a finite field (Wedderburn's theorem);^[1]^[4]

- K is the function field of an algebraic curve over an algebraically closed field (Tsen's theorem);^[4]

- An algebraic extension of Q containing all roots of unity.^[4]

The Brauer group Br(R) of the field R of real numbers is the cyclic group of order two. There are just two non-isomorphic real division algebras with center R: the algebra R itself and the quaternion algebra H.^[5] Since H ⊗ H ≅ M(4,R), the class of H has order two in the Brauer group. More generally, any real closed field has Brauer group of order two.^[1]

K is complete under a discrete valuation with finite residue field. Br(K) is isomorphic to Q/Z.^[5]

Brauer group and class field theory

The notion of Brauer group plays an important role in the modern formulation of the class field theory. If K_v is a non-archimedean local field, the Hasse invariants gives a canonical isomorphism inv_v: Br(K_v) → Q/Z constructed in local class field theory.^[6]^[7]^[8] An element of the Brauer group of order n can be represented by a cyclic division algebra of dimension n².^[9]

The case of a global field K is addressed by the global class field theory. If D is a central simple algebra over K and v is a valuation then D ⊗ K_v is a central simple algebra over K_v, the local completion of K at v. This defines a homomorphism from the Brauer group of K into the Brauer group of K_v. A given central simple algebra D splits for all but finitely many v, so that the image of D under almost all such homomorphisms is 0. The Brauer group Br(K) fits into an exact sequence^[5]^[10]

0\rightarrow \textrm{Br}(K)\rightarrow \bigoplus_{v\in S} \textrm{Br}(K_v)\rightarrow \mathbf{Q}/\mathbf{Z} \rightarrow 0,

where S is the set of all valuations of K and the right arrow is the direct sum of the local invariants: the Brauer group of the real numbers is identified with (1/2)Z/Z. The injectivity of the left arrow is the content of the Albert–Brauer–Hasse–Noether theorem. Exactness in the middle term is a deep fact from the global class field theory. The group Q/Z on the right may be interpreted as the "Brauer group" of the class formation of idele classes associated to K.

Properties

Base change from a field K to an extension field L gives a restriction map from Br(K) to Br(L). The kernel is the group Br(L/K) of classes of K-algebras that split over L.
The Brauer group of any field is a torsion group.^[11]

General theory

For an arbitrary field K, the Brauer group may be expressed in terms of Galois cohomology as follows:^[12]

\textrm{Br}(K) \cong H^2(\textrm{Gal} (K^s/K), {K^s}^*).

Here, K^s is the separable closure of K, which coincides with the algebraic closure when K is a perfect field. Note that every finite dimensional central simple algebra has a separable splitting field.^[13]

The isomorphism of the Brauer group with a Galois cohomology group can be described as follows. If D is a division algebra over K of dimension n² containing a Galois extension L of degree n over K, then the subgroup of elements of D* that normalize L is an extension of the Galois group Gal(L/K) by the nonzero elements L* of L, so corresponds to an element of H²(Gal(L/K), L*).

A generalisation of the Brauer group to the case of commutative rings was introduced by Maurice Auslander and Oscar Goldman,^[14] and more generally for schemes by Alexander Grothendieck. In their approach, central simple algebras over a field are replaced with Azumaya algebras.^[15]

Notes

↑ 1.0 1.1 1.2 Lorenz (2008) p.164
↑ Fried, Michael D.; Jarden, Moshe (2008). Field arithmetic. Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge 11 (3rd revised ed.). Springer-Verlag. p. 209. ISBN 978-3-540-77269-9. Zbl 1145.12001.
↑ Serre (1979) p.161
↑ 4.0 4.1 4.2 Serre (1979) p.162
↑ 5.0 5.1 5.2 Serre (1979) p.163
↑ Lorenz (2008) p.232
↑ Serre (1967) p.137
↑ Shatz (1972) p.155
↑ Lorenz (2008) p.226
↑ Gille & Szamuely (2006) p.159
↑ Lorenz (2008) p.194
↑ Serre (1979) pp.157-159
↑ Jacobson (1996) p.93
↑ Auslander, Maurice; Goldman, Oscar (1961). "The Brauer group of a commutative ring". Trans. Am. Math. Soc. 97: 367–409. doi:10.1090/s0002-9947-1960-0121392-6. ISSN 0002-9947. Zbl 0100.26304.
↑ Saltman (1999) p.21

References

V.A. Iskovskikh (2001), "Brauer group of a field k", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Lorenz, Falko (2008). Algebra. Volume II: Fields with Structure, Algebras and Advanced Topics. Springer. ISBN 978-0-387-72487-4. Zbl 1130.12001.
Gille, Philippe; Szamuely, Tamás (2006). Central simple algebras and Galois cohomology. Cambridge Studies in Advanced Mathematics 101. Cambridge: Cambridge University Press. ISBN 0-521-86103-9. Zbl 1137.12001.
Jacobson, Nathan (1996). Finite-dimensional division algebras over fields. Berlin: Springer-Verlag. ISBN 3-540-57029-2. Zbl 0874.16002.
Pierce, Richard (1982). Associative algebras. Graduate Texts in Mathematics 88. New York-Berlin: Springer-Verlag. ISBN 0-387-90693-2. Zbl 0497.16001.
Reiner, I. (2003). Maximal Orders. London Mathematical Society Monographs. New Series 28. Oxford University Press. pp. 237–241. ISBN 0-19-852673-3. Zbl 1024.16008.
Saltman, David J. (1999). Lectures on division algebras. Regional Conference Series in Mathematics 94. Providence, RI: American Mathematical Society. ISBN 0-8218-0979-2. Zbl 0934.16013.
Serre, Jean-Pierre (1967). "VI. Local class field theory". In Cassels, J.W.S.; Fröhlich, A.. Algebraic number theory. Proceedings of an instructional conference organized by the London Mathematical Society (a NATO Advanced Study Institute) with the support of the International Mathematical Union. London: Academic Press. pp. 128–161. Zbl 0153.07403.
Serre, Jean-Pierre (1979). Local Fields. Graduate Texts in Mathematics 67. Translated from the French by Marvin Jay Greenberg. Springer-Verlag. ISBN 0-387-90424-7. Zbl 0423.12016.
Shatz, Stephen S. (1972). Profinite groups, arithmetic, and geometry. Annals of Mathematics Studies 67. Princeton, NJ: Princeton University Press. ISBN 0-691-08017-8. MR 0347778. Zbl 0236.12002.