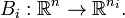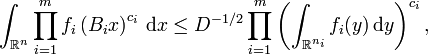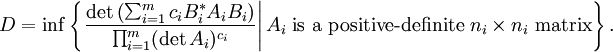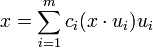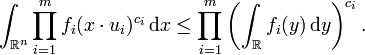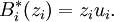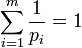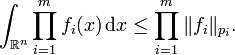Brascamp–Lieb inequality
In mathematics, the Brascamp–Lieb inequality is a result in geometry concerning integrable functions on n-dimensional Euclidean space Rn. It generalizes the Loomis–Whitney inequality and Hölder's inequality, and is named after Herm Jan Brascamp and Elliott H. Lieb. The original inequality (called the geometric inequality here) is in .[1] Its generalization, stated first, is in [2]
Statement of the inequality
Fix natural numbers m and n. For 1 ≤ i ≤ m, let ni ∈ N and let ci > 0 so that
Choose non-negative, integrable functions
and surjective linear maps
Then the following inequality holds:
where D is given by
Another way to state this is that the constant D is what one would obtain by
restricting attention to the case in which each 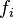 is a centered Gaussian
function, namely
is a centered Gaussian
function, namely 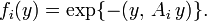
Relationships to other inequalities
The geometric Brascamp–Lieb inequality
The geometric Brascamp–Lieb inequality is a special case of the above, and was used by Ball (1989) to provide upper bounds for volumes of central sections of cubes.
For i = 1, ..., m, let ci > 0 and let ui ∈ Sn−1 be a unit vector; suppose that that ci and ui satisfy
for all x in Rn. Let fi ∈ L1(R; [0, +∞]) for each i = 1, ..., m. Then
The geometric Brascamp–Lieb inequality follows from the Brascamp–Lieb inequality as stated above by taking ni = 1 and Bi(x) = x · ui. Then, for zi ∈ R,
It follows that D = 1 in this case.
Hölder's inequality
As another special case, take ni = n, Bi = id, the identity map on Rn, replacing fi by f1/ci
i, and let ci = 1 / pi for 1 ≤ i ≤ m. Then
and the log-concavity of the determinant of a positive definite matrix implies that D = 1. This yields Hölder's inequality in Rn:
References
- ↑ H.J. Brascamp and E.H. Lieb, Best Constants in Young's Inequality, Its Converse and Its Generalization to More Than Three Functions, Adv. in Math. 20, 151–172 (1976).
- ↑ E.H.Lieb, Gaussian Kernels have only Gaussian Maximizers, Inventiones Mathematicae 102, pp. 179–208 (1990).
- Ball, Keith M. (1989). "Volumes of sections of cubes and related problems". In J. Lindenstrauss and V.D. Milman. Geometric aspects of functional analysis (1987–88). Lecture Notes in Math., Vol. 1376. Berlin: Springer. pp. 251–260.
- Gardner, Richard J. (2002). "The Brunn–Minkowski inequality". Bull. Amer. Math. Soc. (N.S.) 39 (3): pp. 355–405 (electronic). doi:10.1090/S0273-0979-02-00941-2.
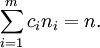
![f_{i} \in L^{1} \left( \mathbb{R}^{n_{i}} ; [0, + \infty] \right)](../I/m/c8a3ae5e95e320686dba457b1553e175.png)