Brams–Taylor procedure
The Brams–Taylor procedure (BTP) is a procedure for envy-free fair cake-cutting. It explicated the first finite procedure to produce an envy-free division of an cake among any positive integer number of players.[1]
History
In 1988, prior to the discovery of the BTP, Sol Garfunkel contended that the problem solved by the theorem, namely n-person envy-free cake-cutting, was among the most important problems in 20th century mathematics.[2]
The BTP was discovered by Steven Brams and Alan D. Taylor. It was first published in the January 1995 issue of American Mathematical Monthly,[3] and later in 1996 in the authors' book.[4]
Brams and Taylor hold a joint US patent from 1999 related to the BTP.[5] [6]
Description
The BTP divides the cake part-by-part. A typical intermediate state of the BTP is as follows:
- A part of the cake, say
, is divided in an envy-free way among all partners. - The rest of the cake, say
, remains undivided, but - - Two partners, say Alice and Bob, has an Irrevocable Advantage (IA) over each other, with respect to . This means that, regardless of how is divided, even if we give entirely to Bob, Alice still doesn't envy Bob, and vice versa.
As an example of how an IA can be generated, consider the first stage of the Selfridge–Conway discrete procedure:
- Alice divides the cake to 3 parts she considers equal; let's call the parts
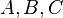. - Bob trims the piece he considers largest (say,
) to make it equal to the second-largest; let's call the trimmings and the trimmed piece 
. - Charlie chooses a piece out of
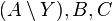; then Bob chooses (he must take 
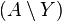if it is available); and lastly Alice.
After this stage is done, all the cake except is divided in an envy-free way. Additionally, Alice now has an IA over whoever took 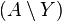. Why? because Alice took either 
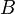or 
, and both of them are equal to in her opinion. So, in Alice's opinion, whoever took 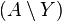can also have - this will not make her envy.
If we want both Alice and Bob to have an IA over each other, a much more complicated procedure is required. It successively divides the cake to smaller and smaller pieces, always giving Alice a piece that she values more than Bob's and vice versa, until the entire cake is divided and an IA is maintained. This might take an unbounded time - depending on the exact valuations of Alice and Bob.
Using the mutual-IA procedure, the main BTP procedure creates IAs for all pairs of partners. For example, when there are 4 partners, there are 6 (unordered) pairs of partners. For each such pair, we run a sub-procedure which guarantees that they have an IA over each other. After every partner has an IA over every other partner, we can just give the remainder to an arbitrary partner and the result is an envy-free division of the entire cake.
See also
- Brams–Taylor–Zwicker procedure - a moving-knife procedure for 4 partners, which uses a finite number of cuts.
References
- ↑ http://m.discovermagazine.com/1995/mar/dividingthespoil479
- ↑ More Equal than Others: Weighted Voting. Sol Garfunkel. For All Practical Purposes. COMAP. 1988
- ↑ Brams, S. J.; Taylor, A. D. (1995). "An Envy-Free Cake Division Protocol". The American Mathematical Monthly 102: 9. doi:10.2307/2974850. JSTOR 2974850.
- ↑ Brams, Steven J.; Taylor, Alan D. Fair Division [From cake-cutting to dispute resolution]. pp. 138–143. ISBN 0521556449.
- ↑ US patent 5983205, Steven J. Brams & Alan D. Taylor, "Computer-based method for the fair division of ownership of goods", issued 1999-11-09, assigned to New York University
- ↑ Brams, Steven J.; Alan D. Taylor (1999-11-09), United States Patent: 5983205 - Computer-based method for the fair division of ownership of goods, retrieved 2014-04-29