Bram van Leer

Bram van Leer

Bram van Leer
Born Netherlands East-Indies
Fields CFD
Fluid dynamics
Numerical Analysis
Institutions University of Michigan
Alma mater Leiden State University
Doctoral advisor Hendrik C. van de Hulst
Known for MUSCL scheme

Bram van Leer is Arthur B. Modine Emeritus Professor of aerospace engineering at the University of Michigan, in Ann Arbor.[1] He specializes in Computational fluid dynamics (CFD), fluid dynamics, and numerical analysis where he has made substantial contributions.

An astrophysicist by education, Van Leer made seminal contributions to CFD in his 5-part article series “Towards the Ultimate Conservative Difference Scheme”, where he extended Godunov’s finite-volume scheme to the second order (MUSCL), developed nonoscillatory interpolation using limiters, an approximate Riemann solver, and Discontinuous-Galerkin schemes for unsteady advection. Since joining the University of Michigan’s Aerospace Engineering Department (1986) he has worked on convergence acceleration by local preconditioning and multigrid relaxation for Euler and Navier-Stokes problems, unsteady adaptive grids, space-environment modeling, atmospheric flow modeling, extended hydrodynamics for rarefied flows, and Discontinuous Galerkin methods. He retired in 2012.

Throughout his career van Leer has crossed interdisciplinary boundaries to export state-of-the-art CFD technology. Starting from astrophysics, he first made an impact on weapons research, followed by aeronautics, then space-weather modeling, atmospheric modeling, surface-water modeling and automotive engine modeling, to name the most important fields.

Research work

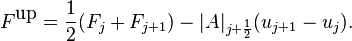
Bram van Leer was a doctoral student in astrophysics at Leiden Observatory (1966-70) when he got interested in Computational Fluid Dynamics (CFD) for the sake of solving cosmic flow problems. His first major result in CFD[2] was the formulation of the upwind numerical flux function for a hyperbolic system of conservation laws: F^\hbox{up} = \frac{1}{2} (F_j + F_{j+1} ) - |A|_{j+\frac{1}{2}} (u_{j+1} - u_j).

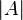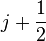Here the matrix |A| appears for the first time, defined as the matrix that has the same eigenvectors as the flux Jacobian A, but the corresponding eigenvalues are the moduli of those of A. The subscript j+\frac{1}{2} indicates a representative or average value on the interval 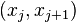(x_j,x_{j+1}); it was no less than 10 years later before Philip L. Roe first presented his much used averaging formulas.

Professor van Leer developed MUSCL scheme, which stands for Monotone Upstream-centered Schemes for Conservation Laws, and the term was introduced by him in a seminal paper (van Leer, 1979).[3] In this paper he constructed the first high-order, total variation diminishing (TVD) scheme where he obtained second order spatial and temporal accuracy. It is a finite volume method that provides high accuracy numerical solutions to partial differential equations which can involve solutions that exhibit shocks, discontinuities, or steep gradients. In 1982 he published another important paper that introduced a computationally efficient alternative, based on flux-vector splitting, to the exact Riemann solver in Godunov algorithm (van Leer, 1982).[4]

The idea is to replace the piecewise constant approximation of Godunov's scheme by reconstructed states, derived from cell-averaged states obtained from the previous time-step. For each cell, slope limited, reconstructed left and right states are obtained and used to calculate fluxes at the cell boundaries (edges). These fluxes are, in turn, used as input to the (approximate) Riemann solver. The Riemann solver solutions are averaged and used to advance the solution in time.

Education and Training

Professional Experience

Honors and Awards

Recent Publications

Personal Interests

Van Leer is also an accomplished musician, playing the piano at the age of 5 and composing at 7. His musical education includes two years at the Royal Conservatory for Music of The Hague, NL. As a pianist he was featured in the Winter '96 issue of Michigan Engineering (Engineering and the Arts); as a carillonist he has played the carillon of the Central Campus Burton Tower on many football Saturdays.

van Leer sitting on a piano at Pierpont Commons, University of Michigan

He was the world's first and only cj (carillon-jockey), based on the North Campus Lurie Tower. In 1993 he gave a full-hour recital on the carillon of the City Hall in Leiden, the town where he studied for many years. Van Leer prefers to improvise in the Dutch carillon-playing style; one of his improvisations is included on a 1998 CD featuring both UM carillons. His carillon composition "Lament" was published in the UM School of Music's carillon music series on the occasion of the Annual Congress of the Guild of Carilloneurs in North America, Ann Arbor, June 2002. A flute composition by Van Leer was performed twice in 1997 by University of Michigan Professor Leone Buyse.

See also

References

  1. ↑ "van Leer at University of Michigan". Retrieved 2009-04-04.
  2. ↑ van Leer, B. (1970). A Choice of Difference Schemes for Ideal Compressible Flow (Ph.D.). Sterrewacht, Leiden, The Netherlands.
  3. ↑ van Leer, B. (1979). "Towards the Ultimate Conservative Difference Scheme, V. A Second Order Sequel to Godunov's Method". J. Comput. Phys. 32 (1): 101–136. Bibcode:1979JCoPh..32..101V. doi:10.1016/0021-9991(79)90145-1.
  4. ↑ van Leer, B. (1982). Flux-vector splitting for the Euler equations, in Lecture Notes in Physics 170. Springer, Berlin. pp. 507–512.

External links