Bowen knot
| Bowen knot | ||
|---|---|---|
 | ||
| style="background:#fee8ab;" text-align: center" colspan="3"| Information | ||
| Family | Bowen Family | |
| Region | Wales | |
The Bowen knot (also known as the heraldic knot in symbolism) is not a true knot, but is rather a heraldic knot, sometimes used as a heraldic charge. It is named after the Welshman James Bowen (died 1629)[1] and is also called true lover’s knot.[1] It consists of a rope in the form of a continuous loop laid out as an upright square shape with loops at each of the four corners.[2] Since the rope is not actually knotted, it would in topological terms be considered an unknot.
An angular Bowen knot is such a knot with no rounded sides, so that it appears to be made of five squares. A lozenge-shaped Bowen knot is called a bendwise Bowen knot or a Bowen cross.
The Bowen knot resembles the symbol ⌘ (Looped square or “St. John’s Arms”), which is used on the command key in some keyboard layouts. However, the origin of this use is not related to the use of the Bowen knot in heraldic designs.
The Dacre, Hungerford, Lacy, Shakespeare, and Tristram knots are all considered variations of the Bowen knot, and are sometimes blazoned as such.
-
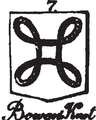
Bowen knot in a book from 1827[1]
-

Angular Bowen knot
-

Bowen cross
- ^ Hugh Clark, A Short and Easy Introduction to Heraldry, London 1827, Part 2, Table 3 Bordures Counterchangings & Lines, fig. 7
References
- ↑ 1.0 1.1 Francis Jones: Bowen of Pentre Ifan and Llwyngwair, in: The Pembrokeshire historian journal of the Pembrokeshire Local History Society, No. 6 (1979), p. 40, online here on the National Library of Wales website: “James Bowen … died at Llwyngwair on 22 October 1629 … The main escutcheon borne on the melancholy occasion showed in the first and fourth quarters, azure a lion rampant or within an orle of roses or, in the second quarter gules a chevron or between three true-love knots or, and in the third quarter, azure a bird standing argent.” (emphasis added)
- ↑ Julian Franklyn, John Tanner: An Encyclopaedic Dictionary of Heraldry, Oxford 1970, p. 47: “a grummet laid out square and turned over at the corners forming external loops.”
Sources
- "Lord Kyl's Heraldry – Glossary – Bo… – Entry: Bowen’s Knot". Lord Padraig MacKay of Kyle. Archived from the original on 2008-10-15. Retrieved 2013-02-15.
- Heraldic Templates — Knots.
| ||||||