Bounding volume

- For building code compliance, see Bounding.
In computer graphics and computational geometry, a bounding volume for a set of objects is a closed volume that completely contains the union of the objects in the set. Bounding volumes are used to improve the efficiency of geometrical operations by using simple volumes to contain more complex objects. Normally, simpler volumes have simpler ways to test for overlap.
A bounding volume for a set of objects is also a bounding volume for the single object consisting of their union, and the other way around. Therefore it is possible to confine the description to the case of a single object, which is assumed to be non-empty and bounded (finite).
Uses of bounding volumes
Bounding volumes are most often used to accelerate certain kinds of tests.
In ray tracing, bounding volumes are used in ray-intersection tests, and in many rendering algorithms, they are used for viewing frustum tests. If the ray or viewing frustum does not intersect the bounding volume, it cannot intersect the object contained in the volume. These intersection tests produce a list of objects that must be displayed. Here, displayed means rendered or rasterized.
In collision detection, when two bounding volumes do not intersect, then the contained objects cannot collide, either.
Testing against a bounding volume is typically much faster than testing against the object itself, because of the bounding volume's simpler geometry. This is because an 'object' is typically composed of polygons or data structures that are reduced to polygonal approximations. In either case, it is computationally wasteful to test each polygon against the view volume if the object is not visible. (Onscreen objects must be 'clipped' to the screen, regardless of whether their surfaces are actually visible.)
To obtain bounding volumes of complex objects, a common way is to break the objects/scene down using a scene graph or more specifically bounding volume hierarchies like e.g. OBB trees. The basic idea behind this is to organize a scene in a tree-like structure where the root comprises the whole scene and each leaf contains a smaller subpart.
Common types of bounding volume
The choice of the type of bounding volume for a given application is determined by a variety of factors: the computational cost of computing a bounding volume for an object, the cost of updating it in applications in which the objects can move or change shape or size, the cost of determining intersections, and the desired precision of the intersection test. The precision of the intersection test is related to the amount of space within the bounding volume not associated with the bounded object, called void space. Sophisticated bounding volumes generally allow for less void space but are more computationally expensive. It is common to use several types in conjunction, such as a cheap one for a quick but rough test in conjunction with a more precise but also more expensive type.
The types treated here all give convex bounding volumes. If the object being bounded is known to be convex, this is not a restriction. If non-convex bounding volumes are required, an approach is to represent them as a union of a number of convex bounding volumes. Unfortunately, intersection tests become quickly more expensive as the bounding boxes become more sophisticated.
A bounding box is a cuboid, or in 2-D a rectangle, containing the object. In dynamical simulation, bounding boxes are preferred to other shapes of bounding volume such as bounding spheres or cylinders for objects that are roughly cuboid in shape when the intersection test needs to be fairly accurate. The benefit is obvious, for example, for objects that rest upon other, such as a car resting on the ground: a bounding sphere would show the car as possibly intersecting with the ground, which then would need to be rejected by a more expensive test of the actual model of the car; a bounding box immediately shows the car as not intersecting with the ground, saving the more expensive test.
In many applications the bounding box is aligned with the axes of the co-ordinate system, and it is then known as an axis-aligned bounding box (AABB). To distinguish the general case from an AABB, an arbitrary bounding box is sometimes called an oriented bounding box (OBB). AABBs are much simpler to test for intersection than OBBs, but have the disadvantage that when the model is rotated they cannot be simply rotated with it, but need to be recomputed.
A bounding capsule is a swept sphere (i.e. the volume that a sphere takes as it moves along a straight line segment) containing the object. Capsules can be represented by the radius of the swept sphere and the segment that the sphere is swept across). It has traits similar to a cylinder, but is easier to use, because the intersection test is simpler. A capsule and another object intersect if the distance between the capsule's defining segment and some feature of the other object is smaller than the capsule's radius. For example, two capsules intersect if the distance between the capsules' segments is smaller than the sum of their radii. This holds for arbitrarily rotated capsules, which is why they're more appealing than cylinders in practice.
A bounding cylinder is a cylinder containing the object. In most applications the axis of the cylinder is aligned with the vertical direction of the scene. Cylinders are appropriate for 3-D objects that can only rotate about a vertical axis but not about other axes, and are otherwise constrained to move by translation only. Two vertical-axis-aligned cylinders intersect when, simultaneously, their projections on the vertical axis intersect – which are two line segments – as well their projections on the horizontal plane – two circular disks. Both are easy to test. In video games, bounding cylinders are often used as bounding volumes for people standing upright.
A bounding ellipsoid is an ellipsoid containing the object. Ellipsoids usually provide tighter fitting than a sphere. Intersections with ellipsoids are done by scaling the other object along the principal axes of the ellipsoid by an amount equal to the multiplicative inverse of the radii of the ellipsoid, thus reducing the problem to intersecting the scaled object with a unit sphere. Care should be taken to avoid problems if the applied scaling introduces skew. Skew can make the usage of ellipsoids impractical in certain cases, for example collision between two arbitrary ellipsoids.
A bounding sphere is a sphere containing the object. In 2-D graphics, this is a circle. Bounding spheres are represented by centre and radius. They are very quick to test for collision with each other: two spheres intersect when the distance between their centres does not exceed the sum of their radii. This makes bounding spheres appropriate for objects that can move in any number of dimensions.
A bounding slab is the volume that projects to an extent on an axis, and can be thought of as the slab bounded between two planes. A bounding box is the intersection of orthogonally oriented bounding slabs. Bounding slabs have been used to speed up ray tracing[1]
A bounding triangle in 2-D is quite useful to speedup the clipping or visibility test of a B-Spline curve. See "Circle and B-Splines clipping algorithms" under the subject Clipping (computer graphics) for an example of use.
A convex hull is the smallest convex volume containing the object. If the object is the union of a finite set of points, its convex hull is a polytope.
A discrete oriented polytope (DOP) generalizes the bounding box. A k-DOP is the Boolean intersection of extents along k directions. Thus, a k-DOP is the Boolean intersection of k bounding slabs and is a convex polytope containing the object (in 2-D a polygon; in 3-D a polyhedron). A 2-D rectangle is a special case of a 2-DOP, and a 3-D box is a special case of a 3-DOP. In general, the axes of a DOP do not have to be orthogonal, and there can be more axes than dimensions of space. For example, a 3-D box that is beveled on all edges and corners can be constructed as a 13-DOP. The actual number of faces can be less than 2 times k if some faces become degenerate, shrunk to an edge or a vertex.
A minimum bounding rectangle or MBR – the least AABB in 2-D – is frequently used in the description of geographic (or "geospatial") data items, serving as a simplified proxy for a dataset's spatial extent (see geospatial metadata) for the purpose of data search (including spatial queries as applicable) and display. It is also a basic component of the R-tree method of spatial indexing.
Basic intersection checks
For some types of bounding volume (OBB and convex polyhedra), an effective check is that of the separating axis theorem. The idea here is that, if there exists an axis by which the objects do not overlap, then the objects do not intersect. Usually the axes checked are those of the basic axes for the volumes (the unit axes in the case of an AABB, or the 3 base axes from each OBB in the case of OBBs). Often, this is followed by also checking the cross-products of the previous axes (one axis from each object).
In the case of an AABB, this tests becomes a simple set of overlap tests in terms of the unit axes. For an AABB defined by M,N against one defined by O,P they do not intersect if (Mx>Px) or (Ox>Nx) or (My>Py) or (Oy>Ny) or (Mz>Pz) or (Oz>Nz).
An AABB can also be projected along an axis, for example, if it has edges of length L and is centered at C, and is being projected along the axis N:
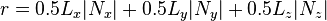 , and
, and 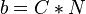 or
or 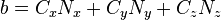 , and
, and 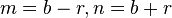 where m and n are the minimum and maximum extents.
where m and n are the minimum and maximum extents.
An OBB is similar in this respect, but is slightly more complicated. For an OBB with L and C as above, and with I, J, and K as the OBB's base axes, then:
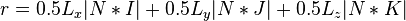
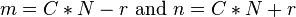
For the ranges m,n and o,p it can be said that they do not intersect if m>p or o>n. Thus, by projecting the ranges of 2 OBBs along the I, J, and K axes of each OBB, and checking for non-intersection, it is possible to detect non-intersection. By additionally checking along the cross products of these axes (I0×I1, I0×J1, ...) one can be more certain that intersection is impossible.
This concept of determining non-intersection via use of axis projection also extends to convex polyhedra, however with the normals of each polyhedral face being used instead of the base axes, and with the extents being based on the minimum and maximum dot products of each vertex against the axes. Note that this description assumes the checks are being done in world space.
See also
- Bounding sphere
- Convex hull algorithms
- Minimum bounding box
- Minimum bounding rectangle
- Spatial index