Borsuk's conjecture

An example of a hexagon cut into three pieces of smaller diameter.

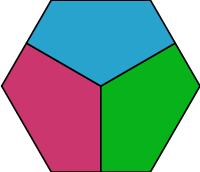
The Borsuk problem in geometry, for historical reasons incorrectly called Borsuk's conjecture, is a question in discrete geometry.

Problem

In 1932 Karol Borsuk showed^[1] that an ordinary 3-dimensional ball in Euclidean space can be easily dissected into 4 solids, each of which has a smaller diameter than the ball, and generally d-dimensional ball can be covered with d + 1 compact sets of diameters smaller than the ball. At the same time he proved that d subsets are not enough in general. The proof is based on the Borsuk–Ulam theorem. That led Borsuk to a general question:

Die folgende Frage bleibt offen: Lässt sich jede beschränkte Teilmenge E des Raumes 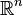in (n + 1) Mengen zerlegen, von denen jede einen kleineren Durchmesser als E hat?^[1]

Translation:

The following question remains open: Can every bounded subset E of the space 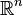be partitioned into (n + 1) sets, each of which has a smaller diameter than E?

The question got a positive answer in the following cases:

• d = 2 — the original result by Borsuk (1932).
• d = 3 — the result of Julian Perkal (1947),^[2] and independently, 8 years later, H. G. Eggleston (1955).^[3] A simple proof was found later by Branko Grünbaum and Aladár Heppes.
• For all d for the smooth convex bodies — the result of Hugo Hadwiger (1946).^[4]
• For all d for centrally-symmetric bodies (A.S. Riesling, 1971).
• For all d for bodies of revolution — the result of Boris Dekster (1995).

The problem was finally solved in 1993 by Jeff Kahn and Gil Kalai, who showed the general answer to Borsuk's question is no. Their construction shows that d + 1 pieces do not suffice for d = 1,325 and for each d > 2,014.

After Andriy V. Bondarenko had shown that Borsuk’s conjecture is false for all d ≥ 65,^[5] the current best bound, due to Thomas Jenrich, is 64.^[6]

Apart from finding the minimum number d of dimensions such that the number of pieces 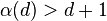mathematicians are interested in finding the general behavior of the function 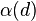. Kahn and Kalai show that in general (that is for d big enough), one needs 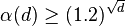number of pieces. They also quote the upper bound by Oded Schramm, who showed that for every ε, if d is sufficiently large, 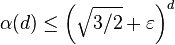. The correct order of magnitude of α(d) is still unknown (see e.g. Alon's article), however it is conjectured that there is a constant c > 1 such that 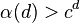for all d ≥ 1.

See also

• Hadwiger's conjecture on covering convex bodies with smaller copies of themselves

Notes

References

• Drei Sätze über die n-dimensionale euklidische Sphäre (German 'Three statements of n-dimensional Euclidean sphere') – original Borsuk's article in Fundamenta Mathematicae, made available by Polish Virtual Library of Science
• Jeff Kahn and Gil Kalai, A counterexample to Borsuk's conjecture, Bulletin of the American Mathematical Society 29 (1993), 60–62.
• Noga Alon, Discrete mathematics: methods and challenges, Proceedings of the International Congress of Mathematicians, Beijing 2002, vol. 1, 119–135.
• Aicke Hinrichs and Christian Richter, New sets with large Borsuk numbers, Discrete Math. 270 (2003), 137–147
• Andrei M. Raigorodskii, The Borsuk partition problem: the seventieth anniversary, Mathematical Intelligencer 26 (2004), no. 3, 4–12.
• Raigorodskii, Andreii M. (2008). "Three lectures on the Borsuk partition problem". In Young, Nicholas; Choi, Yemon. Surveys in contemporary mathematics. London Mathematical Society Lecture Note Series 347. Cambridge University Press. pp. 202–247. ISBN 978-0-521-70564-6. Zbl 1144.52005. 
• Oded Schramm, Illuminating sets of constant width, Mathematika 35 (1988), 180–199.

Further reading

• Oleg Pikhurko, Algebraic Methods in Combinatorics, course notes.

External links

• Weisstein, Eric W., "Borsuk's Conjecture", MathWorld.