Bornological space
In mathematics, particularly in functional analysis, a bornological space is a type of space which, in some sense, possesses the minimum amount of structure needed to address questions of boundedness of sets and functions, in the same way that a topological space possesses the minimum amount of structure needed to address questions of continuity. Bornological spaces were first studied by Mackey and their name was given by Bourbaki.
Bornological sets
Let X be any set. A bornology on X is a collection B of subsets of X such that
- B covers X, i.e.

- B is stable under inclusions, i.e. if A ∈ B and A′ ⊆ A, then A′ ∈ B;
- B is stable under finite unions, i.e. if B1, ..., Bn ∈ B, then

Elements of the collection B are usually called bounded sets. However, if it is necessary to differentiate this formal usage of the term "bounded" with traditional uses, elements of the collection B may also be called bornivorous sets. The pair (X, B) is called a bornological set.
A base of the bornology B is a subset 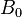 of B such that each element of B is a subset of an element of
of B such that each element of B is a subset of an element of 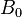 .
.
Examples
- For any set X, the power set of X is a bornology.
- For any set X, the set of finite subsets of X is a bornology. Similarly the set of all at most countably inifinite subsets is a bornology. More generally: The set
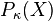 of all subsets of
of all subsets of  having cardinality at most
having cardinality at most 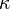 is a bornology.
is a bornology. - For any topological space X that is T1, the set of subsets of X with compact closure is a bornology.
Bounded maps
If 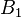 and
and 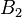 are two bornologies over the spaces
are two bornologies over the spaces  and
and  , respectively, and if
, respectively, and if 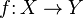 is a function, then we say that
is a function, then we say that  is a bounded map if it maps
is a bounded map if it maps  -bounded sets in
-bounded sets in  to
to 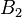 -bounded sets in
-bounded sets in  . If in addition
. If in addition  is a bijection and
is a bijection and 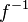 is also bounded then we say that
is also bounded then we say that  is a bornological isomorphism.
is a bornological isomorphism.
Examples:
- If
 and
and  are any two topological vector spaces (they need not even be Hausdorff) and if
are any two topological vector spaces (they need not even be Hausdorff) and if 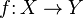 is a continuous linear operator between them, then
is a continuous linear operator between them, then  is a bounded linear operator (when
is a bounded linear operator (when  and
and  have their von-Neumann bornologies). The converse is in general false.
have their von-Neumann bornologies). The converse is in general false.
Theorems:
- Suppose that X and Y are locally convex spaces and that
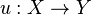 is a linear map. Then the following are equivalent:
is a linear map. Then the following are equivalent:
- u is a bounded map,
- u takes bounded disks to bounded disks,
- For every bornivorous (i.e. bounded in the bornological sense) disk D in Y,
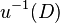 is also bornivorous.
is also bornivorous.
Vector bornologies
If  is a vector space over a field K and then a vector bornology on
is a vector space over a field K and then a vector bornology on  is a bornology B on
is a bornology B on  that is stable under vector addition, scalar multiplication, and the formation of balanced hulls (i.e. if the sum of two bounded sets is bounded, etc.). If in addition B is stable under the formation of convex hulls (i.e. the convex hull of a bounded set is bounded) then B is called a convex vector bornology. And if the only bounded subspace of
that is stable under vector addition, scalar multiplication, and the formation of balanced hulls (i.e. if the sum of two bounded sets is bounded, etc.). If in addition B is stable under the formation of convex hulls (i.e. the convex hull of a bounded set is bounded) then B is called a convex vector bornology. And if the only bounded subspace of  is the trivial subspace (i.e. the space consisting only of
is the trivial subspace (i.e. the space consisting only of 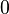 ) then it is called separated. A subset A of B is called bornivorous if it absorbs every bounded set. In a vector bornology, A is bornivorous if it absorbs every bounded balanced set and in a convex vector bornology A is bornivorous if it absorbs every bounded disk.
) then it is called separated. A subset A of B is called bornivorous if it absorbs every bounded set. In a vector bornology, A is bornivorous if it absorbs every bounded balanced set and in a convex vector bornology A is bornivorous if it absorbs every bounded disk.
Bornology of a topological vector space
Every topological vector space X gives a bornology on X by defining a subset 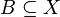 to be bounded (or von-Neumann bounded), if and only if for all open sets
to be bounded (or von-Neumann bounded), if and only if for all open sets 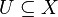 containing zero there exists a
containing zero there exists a 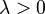 with
with 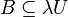 . If X is a locally convex topological vector space then
. If X is a locally convex topological vector space then 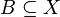 is bounded if and only if all continuous semi-norms on X are bounded on B.
is bounded if and only if all continuous semi-norms on X are bounded on B.
The set of all bounded subsets of X is called the bornology or the Von-Neumann bornology of X.
Induced topology
Suppose that we start with a vector space  and convex vector bornology B on
and convex vector bornology B on  . If we let T denote the collection of all sets that are convex, balanced, and bornivorous then T forms neighborhood basis at 0 for a locally convex topology on
. If we let T denote the collection of all sets that are convex, balanced, and bornivorous then T forms neighborhood basis at 0 for a locally convex topology on  that is compatible with the vector space structure of
that is compatible with the vector space structure of  .
.
Bornological spaces
In functional analysis, a bornological space is a locally convex topological vector space whose topology can be recovered from its bornology in a natural way. Explicitly, a Hausdorff locally convex space  with continuous dual
with continuous dual 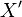 is called a bornological space if any one of the following equivalent conditions holds:
is called a bornological space if any one of the following equivalent conditions holds:
- The locally convex topology induced by the von-Neumann bornology on
 is the same as
is the same as  's initial topology,
's initial topology, - Every bounded semi-norm on
 is continuous,
is continuous, - For all locally convex spaces Y, every bounded linear operator from
 into
into  is continuous.
is continuous. - X is the inductive limit of normed spaces.
- X is the inductive limit of the normed spaces X_D as D varies over the closed and bounded disks of X (or as D varies over the bounded disks of X).
- Every convex, balanced, and bornivorous set in
 is a neighborhood of
is a neighborhood of 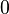 .
. - X carries the Mackey topology
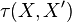 and all bounded linear functionals on X are continuous.
and all bounded linear functionals on X are continuous. -
 has both of the following properties:
has both of the following properties:
-
 is convex-sequential or C-sequential, which means that every convex sequentially open subset of
is convex-sequential or C-sequential, which means that every convex sequentially open subset of  is open,
is open, -
 is sequentially bornological or S-bornological, which means that every convex and bornivorous subset of
is sequentially bornological or S-bornological, which means that every convex and bornivorous subset of  is sequentially open.
is sequentially open.
-
where a subset A of  is called sequentially open if every sequence converging to 0 eventually belongs to A.
is called sequentially open if every sequence converging to 0 eventually belongs to A.
Examples
The following topological vector spaces are all bornological:
- Any metrisable locally convex space is bornological. In particular, any Fréchet space.
- Any LF-space (i.e. any locally convex space that is the strict inductive limit of Fréchet spaces).
- Separated quotients of bornological spaces are bornological.
- The locally convex direct sum and inductive limit of bornological spaces is bornological.
- Fréchet Montel have a bornological strong dual.
Properties
- Given a bornological space X with continuous dual X′, then the topology of X coincides with the Mackey topology τ(X,X′).
- In particular, bornological spaces are Mackey spaces.
- Every quasi-complete (i.e. all closed and bounded subsets are complete) bornological space is barrelled. There exist, however, bornological spaces that are not barrelled.
- Every bornological space is the inductive limit of normed spaces (and Banach spaces if the space is also quasi-complete).
- Let
 be a metrizable locally convex space with continuous dual
be a metrizable locally convex space with continuous dual 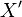 . Then the following are equivalent:
. Then the following are equivalent:
-
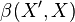 is bornological,
is bornological, -
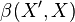 is quasi-barrelled,
is quasi-barrelled, -
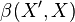 is barrelled,
is barrelled, -
 is a distinguished space.
is a distinguished space.
-
- If
 is bornological,
is bornological,  is a locally convex TVS, and
is a locally convex TVS, and 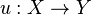 is a linear map, then the following are equivalent:
is a linear map, then the following are equivalent:
-
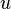 is continuous,
is continuous, - for every set
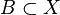 that's bounded in
that's bounded in  ,
, 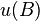 is bounded,
is bounded, - If
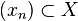 is a null sequence in
is a null sequence in  then
then  is a null sequence in
is a null sequence in  .
.
-
- The strong dual of a bornological space is complete, but it need not be bornological.
- Closed subspaces of bornological space need not be bornological.
Banach disks
Suppose that X is a topological vector space. Then we say that a subset D of X is a disk if it is convex and balanced. The disk D is absorbing in the space span(D) and so its Minkowski functional forms a seminorm on this space, which is denoted by 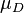 or by
or by  . When we give span(D) the topology induced by this seminorm, we denote the resulting topological vector space by
. When we give span(D) the topology induced by this seminorm, we denote the resulting topological vector space by  . A basis of neighborhoods of 0 of this space consists of all sets of the form r D where r ranges over all positive real numbers.
. A basis of neighborhoods of 0 of this space consists of all sets of the form r D where r ranges over all positive real numbers.
This space is not necessarily Hausdorff as is the case, for instance, if we let 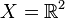 and D be the x-axis. However, if D is a bounded disk and if X is Hausdorff, then
and D be the x-axis. However, if D is a bounded disk and if X is Hausdorff, then 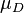 is a norm and
is a norm and  is a normed space. If D is a bounded sequentially complete disk and X is Hausdorff, then the space
is a normed space. If D is a bounded sequentially complete disk and X is Hausdorff, then the space  is a Banach space. A bounded disk in X for which
is a Banach space. A bounded disk in X for which  is a Banach space is called a Banach disk, infracomplete, or a bounded completant.
is a Banach space is called a Banach disk, infracomplete, or a bounded completant.
Suppose that X is a locally convex Hausdorff space and that D is a bounded disk in X. Then
- If D is complete in X and T is a Barrell in X, then there is a number r > 0 such that
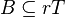 .
.
Examples
- Any closed and bounded disk in a Banach space is a Banach disk.
- If U is a convex balanced closed neighborhood of 0 in X then the collection of all neighborhoods r U, where r > 0 ranges over the positive real numbers, induces a topological vector space topology on X. When X has this topology, it is denoted by X_U. Since this topology is not necessarily Hausdorff nor complete, the completion of the Hausdorff space
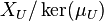 is denoted by
is denoted by 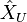 so that
so that 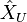 is a complete Hausdorff space and
is a complete Hausdorff space and 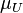 is a norm on this space making
is a norm on this space making 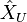 into a Banach space. The polar of U,
into a Banach space. The polar of U, 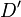 , is a weakly compact bounded equicontinuous disk in
, is a weakly compact bounded equicontinuous disk in 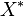 and so is infracomplete.
and so is infracomplete.
Ultrabornological spaces
A disk in a topological vector space X is called infrabornivorous if it absorbs all Banach disks. If X is locally convex and Hausdorff, then a disk is infrabornivorous if and only if it absorbs all compact disks. A locally convex space is called ultrabornological if any of the following conditions hold:
- every infrabornivorous disk is a neighborhood of 0,
- X be the inductive limit of the spaces
 as D varies over all compact disks in X,
as D varies over all compact disks in X, - A seminorm on X that is bounded on each Banach disk is necessarily continuous,
- For every locally convex space Y and every linear map
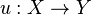 , if u is bounded on each Banach disk then u is continuous.
, if u is bounded on each Banach disk then u is continuous. - For every Banach space Y and every linear map
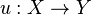 , if u is bounded on each Banach disk then u is continuous.
, if u is bounded on each Banach disk then u is continuous.
Properties
- The finite product of ultrabornological spaces is ultrabornological.
- Inductive limits of ultrabornological spaces are ultrabornological.
See also
- Space of linear maps
References
- Hogbe-Nlend, Henri (1977). Bornologies and functional analysis. Amsterdam: North-Holland Publishing Co. pp. xii+144. ISBN 0-7204-0712-5. MR 0500064.
- H.H. Schaefer (1970). Topological Vector Spaces. GTM 3. Springer-Verlag. pp. 61–63. ISBN 0-387-05380-8.
- Khaleelulla, S.M. (1982). Counterexamples in Topological Vector Spaces. GTM 936. Berlin Heidelberg: Springer-Verlag. pp. 29–33, 49, 104. ISBN 9783540115656.
| ||||||||||||||||||||||||||||||||||