Born series
The Born series[1] is the expansion of different scattering quantities in quantum scattering theory in the powers of the interaction potential 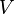 (more precisely in powers of
(more precisely in powers of 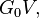 where
where 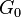 is the free particle Green's operator). It is closely related to Born approximation, which is the first order term of the Born series. The series can formally be understood as power series introducing the coupling constant by substitution
is the free particle Green's operator). It is closely related to Born approximation, which is the first order term of the Born series. The series can formally be understood as power series introducing the coupling constant by substitution 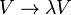 . The speed of convergence and radius of convergence of the Born series are related to eigenvalues of the operator
. The speed of convergence and radius of convergence of the Born series are related to eigenvalues of the operator 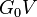 . In general the first few terms of the Born series are good approximation to the expanded quantity for "weak" interaction
. In general the first few terms of the Born series are good approximation to the expanded quantity for "weak" interaction 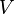 and large collision energy.
and large collision energy.
Born series for scattering states
The Born series for the scattering states reads
It can be derived by itrating the Lippmann–Schwinger equation
Note that the Green's operator 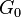 for free partice can be retarded/advanced or standing wave operator for retarded
for free partice can be retarded/advanced or standing wave operator for retarded 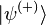 advanced
advanced 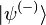 or standing wave scattering states
or standing wave scattering states 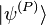 .
The first iteration is obtained by replacing the full scattering solution
.
The first iteration is obtained by replacing the full scattering solution 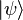 with free particle wave function
with free particle wave function 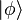 on the right hand side of the Lippmann-Schwinger equation and it gives the first Born approximation.
The second iteration substitutes the first Born approximation in the right hand side and the result is called the second Born approximation. In general the n-th Born approximation takes n-terms of the series into account. The second Born approximation is sometimes used, when the first Born approximation wanishes, but the higher terms are rarely used. The Born series can formally be summed as geometric series with the common ratio equal to the operator
on the right hand side of the Lippmann-Schwinger equation and it gives the first Born approximation.
The second iteration substitutes the first Born approximation in the right hand side and the result is called the second Born approximation. In general the n-th Born approximation takes n-terms of the series into account. The second Born approximation is sometimes used, when the first Born approximation wanishes, but the higher terms are rarely used. The Born series can formally be summed as geometric series with the common ratio equal to the operator 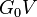 , giving the formal solution to Lippmann-Schwinger equation in the form
, giving the formal solution to Lippmann-Schwinger equation in the form
Born series for T-matrix
The Born series can also be written for other scattering quantities like the T-matrix which is closely related to the scattering amplitude. Iterating Lippmann-Schwinger equation for the T-matrix we get
For the T-matrix 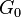 stands only for retarded Green's operator
stands only for retarded Green's operator 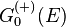 . The standing wave Green's operator would give the K-matrix instead.
. The standing wave Green's operator would give the K-matrix instead.
Born series for full Green's operator
The Lippmann-Schwinger equation for Green's operator is called resolvent identity
Its solution by iterations leads to Born series for the full Green's operator 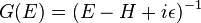
See also
- Lippmann-Schwinger equation
- Quantum scattering theory
- T-matrix
- Green's operator
Bibliography
- Joachain, Charles J. (1983). Quantum collision theory. North Holland. ISBN 0-7204-0294-8.
- Taylor, John R. (1972). Scattering Theory: The Quantum Theory on Nonrelativistic Collisions. John Wiley. ISBN 0-471-84900-6.
- Newton, Roger G. (2002). Scattering Theory of Waves and Particles. Dover Publications, inc. ISBN 0-486-42535-5.
References
- ↑ Born, Max (1926). Zeitschrift fur physik 38: 803. Missing or empty
|title=(help)
![|\psi\rangle = |\phi \rangle + G_0(E) V |\phi\rangle + [G_0(E) V]^2 |\phi\rangle + [G_0(E) V]^3 |\phi\rangle + \dots](../I/m/07457757ea1431ec740384d85147284b.png)
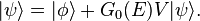
![|\psi\rangle = [I - G_0(E) V]^{-1} |\phi \rangle = [V - VG_0(E) V]^{-1} V |\phi \rangle .](../I/m/ba97372ec06da1358e36e8fb1ecf4493.png)
![T(E) = V + V G_0(E) V + V [G_0(E) V]^2 + V [G_0(E) V]^3 + \dots](../I/m/f04e2ac24fa8d04eb255e20c1ea6044b.png)
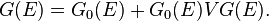
![G(E) = G_0(E) + G_0(E) V G_0(E) + [G_0(E) V]^2 G_0(E) + [G_0(E) V]^3 G_0(E) + \dots](../I/m/6edbe8e1220f7301a473014b5e2a10b1.png)