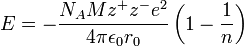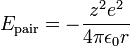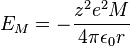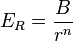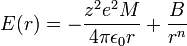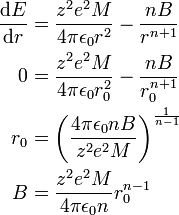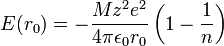Born–Landé equation

The Born–Landé equation is a means of calculating the lattice energy of a crystalline ionic compound. In 1918[1] Max Born and Alfred Landé proposed that the lattice energy could be derived from the electrostatic potential of the ionic lattice and a repulsive potential energy term.[2]

E =- \frac{N_AMz^+z^- e^2 }{4 \pi \epsilon_0 r_0}\left(1-\frac{1}{n}\right)

where:

Derivation

The ionic lattice is modeled as an assembly of hard elastic spheres which are compressed together by the mutual attraction of the electrostatic charges on the ions. They achieve the observed equilibrium distance apart due to a balancing short range repulsion.

Electrostatic potential

The electrostatic potential energy, 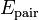E_\text{pair}, between a pair of ions of equal and opposite charge is:

E_\text{pair} = -\frac{z^2 e^2 }{4 \pi \epsilon_0 r}

where

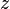z = magnitude of charge on one ion
e = elementary charge, 1.6022×10−19 C
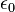\epsilon_0 = permittivity of free space
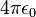4\pi \epsilon_0 = 1.112×10−10 C²/(J m)
r = distance separating the ion centers

For a simple lattice consisting ions with equal and opposite charge in a 1:1 ratio, interactions between one ion and all other lattice ions need to be summed to calculate 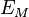E_M, sometimes called the Madelung or lattice energy:

E_M = -\frac{z^2 e^2 M}{4 \pi \epsilon_0 r}

where

M = Madelung constant, which is related to the geometry of the crystal
r = closest distance between two ions of opposite charge

Repulsive term

Born and Lande suggested that a repulsive interaction between the lattice ions would be proportional to 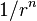1/r^n so that the repulsive energy term, 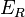E_R, would be expressed:

\,E_R = \frac{B}{r^n}

where

B = constant scaling the strength of the repulsive interaction
r = closest distance between two ions of opposite charge
n = Born exponent, a number between 5 and 12 expressing the steepness of the repulsive barrier

Total energy

The total intensive potential energy of an ion in the lattice can therefore be expressed as the sum of the Madelung and repulsive potentials:

E(r) = -\frac{z^2 e^2 M}{4 \pi \epsilon_0 r} + \frac{B}{r^n}

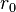Minimizing this energy with respect to r yields the equilibrium separation r_0 in terms of the unknown constant B:

\begin{align} \frac{\mathrm{d}E}{\mathrm{d}r} &= \frac{z^2 e^2 M}{4 \pi \epsilon_0 r^2} - \frac{n B}{r^{n+1}} \\ 0 &= \frac{z^2 e^2 M}{4 \pi \epsilon_0 r_0^2} - \frac{n B}{r_0^{n+1}} \\ r_0 &= \left( \frac{4 \pi \epsilon_0 n B}{z^2 e^2 M}\right) ^\frac{1}{n-1} \\ B &= \frac{z^2 e^2 M}{4 \pi \epsilon_0 n} r_0^{n-1} \end{align}

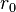Evaluating the minimum intensive potential energy and substituting the expression for B in terms of r_0 yields the Born–Landé equation:

E(r_0) = - \frac{M z^2 e^2 }{4 \pi \epsilon_0 r_0}\left(1-\frac{1}{n}\right)

Calculated lattice energies

The Born–Landé equation gives a reasonable fit to the lattice energy [2]

Compound Calculated Lattice Energy Experimental Lattice Energy
NaCl −756 kJ/mol −787 kJ/mol
LiF −1007 kJ/mol −1046 kJ/mol
CaCl2 −2170 kJ/mol −2255 kJ/mol

Born Exponent

The Born exponent is typically between 5 and 12. Approximate experimental values are listed below:[4]

Ion configuration He Ne Ar, Cu+ Kr, Ag+ Xe, Au+
n 5 7 9 10 12

See also

References

  1. ↑ Brown, I. David (2002). The chemical bond in inorganic chemistry : the bond valence model (Reprint. ed.). New York: Oxford University Press. ISBN 0-19-850870-0.
  2. ↑ 2.0 2.1 Johnson, the Open University ; RSC ; edited by David (2002). Metals and chemical change (1. publ. ed.). Cambridge: Royal Society of Chemistry. ISBN 0-85404-665-8.
  3. ↑ Cotton, F. Albert; Wilkinson, Geoffrey (1980), Advanced Inorganic Chemistry (4th ed.), New York: Wiley, ISBN 0-471-02775-8
  4. ↑ "Lattice Energy".