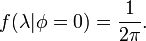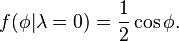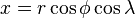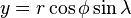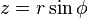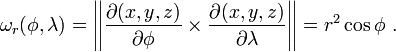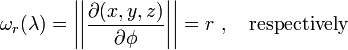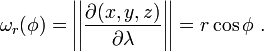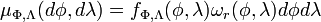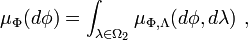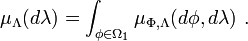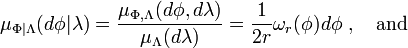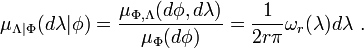Borel–Kolmogorov paradox
In probability theory, the Borel–Kolmogorov paradox (sometimes known as Borel's paradox) is a paradox relating to conditional probability with respect to an event of probability zero (also known as a null set). It is named after Émile Borel and Andrey Kolmogorov.
A great circle puzzle
Suppose that a random variable has a uniform distribution on a unit sphere. What is its conditional distribution on a great circle? Because of the symmetry of the sphere, one might expect that the distribution is uniform and independent of the choice of coordinates. However, two analyses give contradictory results. First, note that choosing a point uniformly on the sphere is equivalent to choosing the longitude λ uniformly from [-π,π] and choosing the latitude φ from [-π/2,π/2] with density 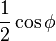 .[1] Then we can look at two different great circles:
.[1] Then we can look at two different great circles:
- 1. If the coordinates are chosen so that the great circle is an equator (latitude φ = 0), the conditional density for a longitude λ defined on the interval [–π,π] is
- 2. If the great circle is a line of longitude with λ = 0, the conditional density for φ on the interval [–π/2,π/2] is
One distribution is uniform on the circle, the other is not. Yet both seem to be referring to the same great circle in different coordinate systems.
Many quite futile arguments have raged - between otherwise competent probabilists - over which of these results is 'correct'.
—E.T. Jaynes[1]
Explanation and implications
In case (1) above, the conditional probability that the longitude λ lies in a set E given that φ = 0 can be written P(λ ∈ E | φ = 0). Elementary probability theory suggests this can be computed as P(λ ∈ E and φ=0)/P(φ=0), but that expression is not well-defined since P(φ=0) = 0. Measure theory provides a way to define a conditional probability, using the family of events Rab = {φ : a < φ < b} which are horizontal rings consisting of all points with latitude between a and b.
The resolution of the paradox is to notice that in case (2), P(φ ∈ F | λ=0) is defined using the events Lab = {λ : a < λ < b}, which are lunes (vertical wedges), consisting of all points whose longitude varies between a and b. So although P(λ ∈ E | φ=0) and P(φ ∈ F | λ=0) each provide a probability distribution on a great circle, one of them is defined using rings, and the other using lunes. Thus it is not surprising after all that P(λ ∈ E | φ=0) and P(φ ∈ F | λ=0) have different distributions.
The concept of a conditional probability with regard to an isolated hypothesis whose probability equals 0 is inadmissible. For we can obtain a probability distribution for [the latitude] on the meridian circle only if we regard this circle as an element of the decomposition of the entire spherical surface onto meridian circles with the given poles
… the term 'great circle' is ambiguous until we specify what limiting operation is to produce it. The intuitive symmetry argument presupposes the equatorial limit; yet one eating slices of an orange might presuppose the other.
—E.T. Jaynes[1]
Mathematical explication
To understand the problem we need to recognize that a distribution on a continuous random variable is described by a density f only with respect to some measure μ. Both are important for the full description of the probability distribution. Or, equivalently, we need to fully define the space on which we want to define f.
Let Φ and Λ denote two random variables taking values in Ω1 = [-π/2,π/2] respectively Ω2 = [-π,π]. An event {Φ=φ,Λ=λ} gives a point on the sphere S(r) with radius r. We define the coordinate transform
for which we obtain the volume element
Furthermore, if either φ or λ is fixed, we get the volume elements
Let
denote the joint measure on 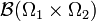 , which has a density
, which has a density 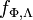 with respect to
with respect to 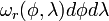 and let
and let
If we assume that the density 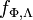 is uniform, then
is uniform, then
Hence, 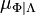 has a uniform density with respect to
has a uniform density with respect to 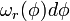 but not with respect to the Lebesgue measure. On the other hand,
but not with respect to the Lebesgue measure. On the other hand, 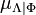 has a uniform density with respect to
has a uniform density with respect to 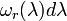 and the Lebesgue measure.
and the Lebesgue measure.
Notes
- ↑ 1.0 1.1 1.2 Jaynes 2003, pp. 1514–1517
- ↑ Originally Kolmogorov (1933), translated in Kolmogorov (1956). Sourced from Pollard (2002)
References and further reading
- Jaynes, E.T. (2003). "15.7 The Borel-Kolmogorov paradox". Probability Theory: The Logic of Science. Cambridge University Press. pp. 467–470. ISBN 0-521-59271-2. MR 1992316.
- Kolmogorov, Andrey (1933). Grundbegriffe der Wahrscheinlichkeitsrechnung (in German). Berlin: Julius Springer.
- Translation: Kolmogorov, Andrey (1956). "Chapter V, §2. Explanation of a Borel Paradox". Foundations of the Theory of Probability (2nd ed.). New York: Chelsea. pp. 50–51. ISBN 0-8284-0023-7.
- Pollard, David (2002). "Chapter 5. Conditioning, Example 17.". A User's Guide to Measure Theoretic Probability. Cambridge University Press. pp. 122–123. ISBN 0-521-00289-3. MR 1873379.
- Mosegaard, K., & Tarantola, A. (2002). 16 Probabilistic approach to inverse problems. International Geophysics, 81, 237-265.