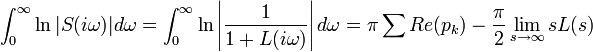Bode's sensitivity integral
Bode's sensitivity integral, discovered by Hendrik Wade Bode, is a formula that quantifies some of the limitations in feedback control of linear parameter invariant systems. Let L be the loop transfer function and S be the sensitivity function. Then the following holds:
where 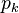 are the poles of L in the right half plane (unstable poles).
are the poles of L in the right half plane (unstable poles).
If L has at least two more poles than zeros, and has no poles in the right half plane (is stable), the equation simplifies to:
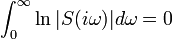
This equality shows that if sensitivity to disturbance is suppressed at some frequency range, it is necessarily increased at some other range. This has been called the "waterbed effect."[1]
References
Further reading
- Karl Johan Åström and Richard M. Murray. Feedback Systems: An Introduction for Scientists and Engineers. Chapter 11 - Frequency Domain Design. Princeton University Press, 2008. http://www.cds.caltech.edu/~murray/amwiki/Frequency_Domain_Design