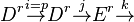Bockstein spectral sequence
In mathematics, the Bockstein spectral sequence is a spectral sequence relating the homology with mod p coefficients and the homology reduced mod p. It is named after Meyer Bockstein.
Definition
Let C be a chain complex of torsion-free abelian groups and p a prime number. Then we have the exact sequence:
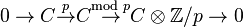 .
.
Taking integral homology H, we get the exact couple of "doubly graded" abelian groups:
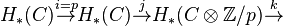 .
.
where the grading goes: 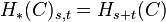 and the same for
and the same for 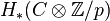 ,
, 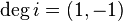 ,
, 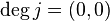 ,
, 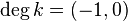 .
.
This gives the first page of the spectral sequence: we take 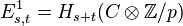 with the differential
with the differential 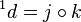 . The derived couple of the above exact couple then gives the second page and so forth. Explicitly, we have
. The derived couple of the above exact couple then gives the second page and so forth. Explicitly, we have 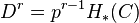 that fits into the exact couple:
that fits into the exact couple:
where 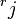 is
is 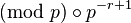 and
and 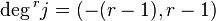 (the degrees of i, k are the same as before). Now, taking
(the degrees of i, k are the same as before). Now, taking 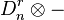 of
of 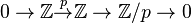 , we get:
, we get:
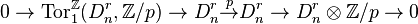 .
.
This tells the kernel and cokernel of 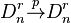 . Expanding the exact couple into a long exact sequence, we get: for any r,
. Expanding the exact couple into a long exact sequence, we get: for any r,
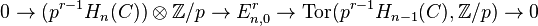 .
.
When 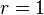 , this is the same thing as the universal coefficient theorem for homology.
, this is the same thing as the universal coefficient theorem for homology.
Assume the abelian group 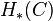 is finitely generated; in particular, only finitely many cyclic modules of the form
is finitely generated; in particular, only finitely many cyclic modules of the form 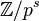 can appear as a direct summand of
can appear as a direct summand of 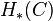 . Letting
. Letting 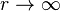 we thus see
we thus see 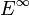 is isomorphic to
is isomorphic to 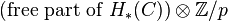 .
.
References
- McCleary, John (2001), A User's Guide to Spectral Sequences, Cambridge Studies in Advanced Mathematics 58 (2nd ed.), Cambridge University Press, doi:10.2277/0521567599, ISBN 978-0-521-56759-6, MR 1793722
- J. P. May, A primer on spectral sequences