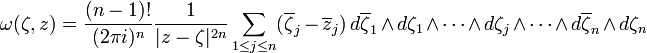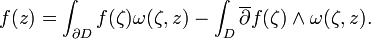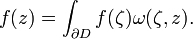Bochner–Martinelli formula
In mathematics, the Bochner–Martinelli formula is a generalization of the Cauchy integral formula to functions of several complex variables, introduced by Enzo Martinelli (1938) and Salomon Bochner (1943).
History
Formula (53) of the present paper and a proof of theorem 5 based on it have just been published by Enzo Martinelli (...).[1] The present author may be permitted to state that these results have been presented by him in a Princeton graduate course in Winter 1940/1941 and were subsequently incorporated, in a Princeton doctorate thesis (June 1941) by Donald C. May, entitled: An integral formula for analytic functions of k variables with some applications.
However this author's claim in loc. cit. footnote 1,[2] that he might have been familiar with the general shape of the formula before Martinelli, was wholly unjustified and is hereby being retracted.
Bochner–Martinelli kernel
For ζ, z in ℂn the Bochner–Martinelli kernel ω(ζ,z) is a differential form in ζ of bidegree (n,n−1) defined by
(where the term dζj is omitted).
Suppose that f is a continuously differentiable function on the closure of a domain D in ℂn with piecewise smooth boundary ∂D. Then the Bochner–Martinelli formula states that if z is in the domain D then
In particular if f is holomorphic the second term vanishes, so
See also
Notes
- ↑ Bochner refers explicitly to the article (Martinelli 1942-1943), apparently being not aware of the earlier one (Martinelli 1938), which actually contains Martinelli's proof of the formula. However, the earlier article is explicitly cited in the later one, as it can be seen from (Martinelli 1942-1943, p. 340, footnote 2).
- ↑ Bochner refers to his claim in (Bochner 1943, p. 652, footnote 1).
References
- Aizenberg, L. A.; Yuzhakov, A. P. (1983) [1979], Integral Representations and Residues in Multidimensional Complex Analysis, Translations of Mathematical Monographs 58, Providence R.I.: American Mathematical Society, pp. x+283, ISBN 0-8218-4511-X, MR 0735793, Zbl 0537.32002
- Bochner, Salomon (1943), "Analytic and meromorphic continuation by means of Green's formula", Annals of Mathematics, Second Series 44: 652–673, ISSN 0003-486X, JSTOR 1969103, MR 0009206, Zbl 0060.24206.
- Bochner, Salomon (1947), "On compact complex manifolds", The Journal of the Indian Mathematical Society, New Series, 11: 1–21, MR 0023919, Zbl 0038.23701.
- Chirka, E.M. (2001), "Bochner–Martinelli representation formula", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Krantz, Steven G. (2001) [1992], Function theory of several complex variables (reprint of 2nd ed.), Providence, R.I.: AMS Chelsea Publishing, pp. xvi+564, ISBN 978-0-8218-2724-6, MR 1846625, Zbl 1087.32001.
- Kytmanov, Alexander M. (1995) [1992], The Bochner-Martinelli integral and its applications, Birkhäuser Verlag, pp. xii+305, ISBN 978-3-7643-5240-0, MR 1409816, Zbl 0834.32001.
- Kytmanov, Alexander M.; Myslivets, Simona G. (2010), Интегральные представления и их приложения в многомерном комплексном анализе, Красноярск: СФУ, p. 389, ISBN 978-5-7638-1990-8 (English translation of title:"Integral representations and their application in multidimensional complex analysis").
- Martinelli, Enzo (1938), "Alcuni teoremi integrali per le funzioni analitiche di più variabili complesse", Memorie della Reale Accademia d'Italia (in Italian) 9: 269–283, JFM 64.0322.04, Zbl 0022.24002. "Some integral theorems for analytic functions of several complex variables" (English translation of the title) is the first paper where the now called Bochner–Martinelli formula is introduced and proved.
- Martinelli, Enzo (1942–1943), "Sopra una dimostrazione di R. Fueter per un teorema di Hartogs", Commentarii Mathematici Helvetici (in Italian) 15 (1): 340–349, doi:10.5169/seals-14896, MR 0010729, Zbl 0028.15201. Available at the SEALS Portal. In the work "On a proof of R. Fueter of a theorem of Hartogs" (English translation of the title), Martinelli gave a proof of Hartogs' extension theorem by using the Bochner–Martinelli formula.
- Martinelli, Enzo (1984), Introduzione elementare alla teoria delle funzioni di variabili complesse con particolare riguardo alle rappresentazioni integrali, Contributi del Centro Linceo Interdisciplinare di Scienze Matematiche e Loro Applicazioni (in Italian) 67, Rome: Accademia Nazionale dei Lincei, pp. 236+II. "Elementary introduction to the theory of functions of complex variables with particular regard to integral representations" (English translation of the title reads) is a textbook, published by the Accademia Nazionale dei Lincei, taken from the notes from a course held by Martinelli when he was in charge to the academy as a "Professore Linceo".