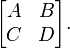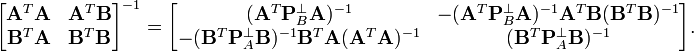Block matrix pseudoinverse
In mathematics, block matrix pseudoinverse is a formula of pseudoinverse of a partitioned matrix. This is useful for decomposing or approximating many algorithms updating parameters in signal processing, which are based on least squares method.
Derivation
Consider a column-wise partitioned matrix:
If the above matrix is full rank, the pseudoinverse matrices of it and its transpose are as follows.
The pseudoinverse requires (n + p)-square matrix inversion.
To reduce complexity and introduce parallelism, we derive the following decomposed formula. From a block matrix inverse![\mathbf ([\mathbf A, \mathbf B]^T [\mathbf A, \mathbf B])^{-1}](../I/m/eccca8c6c23cc9a9d29843d7889061bc.png) , we can have
, we can have
where orthogonal projection matrices are defined by
Interestingly, from the idempotence of projection matrix, we can verify that the pseudoinverse of block matrix consists of pseudoinverse of projected matrices:
Thus, we decomposed the block matrix pseudoinverse into two submatrix pseudoinverses, which cost n- and p-square matrix inversions, respectively.
Note that the above formulae are not necessarily valid if ![[\mathbf A, \mathbf B]](../I/m/3cd11b618b99bcb6f105f1ef656e2f10.png) does not have full rank – for example, if
does not have full rank – for example, if 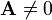 , then
, then
Application to least squares problems
Given the same matrices as above, we consider the following least squares problems, which appear as multiple objective optimizations or constrained problems in signal processing. Eventually, we can implement a parallel algorithm for least squares based on the following results.
Column-wise partitioning in over-determined least squares
Suppose a solution
 solves an over-determined system:
solves an over-determined system:
Using the block matrix pseudoinverse, we have
Therefore, we have a decomposed solution:
Row-wise partitioning in under-determined least squares
Suppose a solution 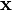 solves an under-determined system:
solves an under-determined system:
The minimum-norm solution is given by
Using the block matrix pseudoinverse, we have
Comments on matrix inversion
Instead of ![\mathbf ([\mathbf A, \mathbf B]^T [\mathbf A, \mathbf B])^{-1}](../I/m/eccca8c6c23cc9a9d29843d7889061bc.png) ,
we need to calculate directly or indirectly
,
we need to calculate directly or indirectly
In a dense and small system, we can use singular value decomposition, QR decomposition, or Cholesky decomposition to replace the matrix inversions with numerical routines. In a large system, we may employ iterative methods such as Krylov subspace methods.
Considering parallel algorithms, we can compute  and
and
 in parallel. Then, we finish to compute
in parallel. Then, we finish to compute 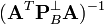 and
and  also in parallel.
also in parallel.
Block matrix inversion
Let a block matrix be
We can get an inverse formula by combining the previous results in.[1]
where  and
and 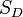 , respectively, Schur complements of
, respectively, Schur complements of 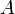 and
and 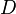 , are defined by
, are defined by  , and
, and  . This relation is derived by using Block Triangular
Decomposition. It is called simple block matrix inversion.[2]
. This relation is derived by using Block Triangular
Decomposition. It is called simple block matrix inversion.[2]
Now we can obtain the inverse of the symmetric block matrix:
Since the block matrix is symmetric, we also have
Then, we can see how the Schur complements are connected to the projection matrices of the symmetric, partitioned matrix.
See also
References
- ↑ Smith, Julius O. "Block matrix decompositions". Archived from the original on 2008-09-15.
- ↑ S. Jo, S. W. Kim and T. J. Park, "Equally constrained affine projection algorithm," in Conference Record of the Thirty-Eighth Asilomar Conference on Signals, Systems and Computers, vol. 1, pp. 955–959, Nov. 7–10, 2004.
External links
- The Matrix Reference Manual by Mike Brookes
- Linear Algebra Glossary by John Burkardt
- The Matrix Cookbook by Kaare Brandt Petersen
- Lecture 8: Least-norm solutions of undetermined equations by Stephen P. Boyd
| ||||||||||||||||||
![[\mathbf A, \mathbf B], \qquad \mathbf A \in \reals^{m\times n}, \qquad \mathbf B \in \reals^{m\times p}, \qquad m \geq n+p.](../I/m/7efc0e8cefa8864f837646e239502a55.png)
![\begin{bmatrix}
\mathbf A, & \mathbf B
\end{bmatrix}
^{+} = ([\mathbf A, \mathbf B]^T [\mathbf A, \mathbf B])^{-1} [\mathbf A, \mathbf B]^T,](../I/m/ea8512cde6efaa5804a4f3885e650816.png)
![\begin{bmatrix}
\mathbf A^T \\ \mathbf B^T
\end{bmatrix}
^{+} = [\mathbf A, \mathbf B] ([\mathbf A, \mathbf B]^T [\mathbf A, \mathbf B])^{-1}.](../I/m/8be8a16fae751075f85ba279bdf5fd00.png)
![\begin{bmatrix}
\mathbf A, & \mathbf B
\end{bmatrix}
^{+} = \left[\mathbf P_B^\perp \mathbf A( \mathbf A^T \mathbf P_B^\perp \mathbf A)^{-1}, \quad \mathbf P_A^\perp \mathbf B(\mathbf B^T \mathbf P_A^\perp \mathbf B)^{-1}\right]^T,](../I/m/8314f0e5d135b9a9f11841b02bcfa368.png)
![\begin{bmatrix}
\mathbf A^T \\ \mathbf B^T
\end{bmatrix}
^{+} = \left[\mathbf P_B^\perp \mathbf A( \mathbf A^T \mathbf P_B^\perp \mathbf A)^{-1}, \quad \mathbf P_A^\perp \mathbf B(\mathbf B^T \mathbf P_A^\perp \mathbf B)^{-1}\right],](../I/m/54b8a450c68bc7070bf4f623c0f0a75d.png)
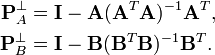
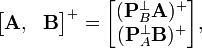
![\begin{bmatrix}
\mathbf A^T \\ \mathbf B^T
\end{bmatrix}
^{+}
= [(\mathbf A^T \mathbf P_B^{\perp})^{+},
\quad (\mathbf B^T \mathbf P_A^{\perp})^{+} ].](../I/m/770ce758b3d5e1b812a12b0196fb0342.png)

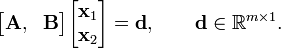
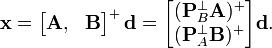

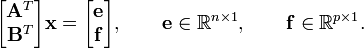

![\mathbf x
=
[(\mathbf A^T\mathbf P_B^{\perp})^{+},
\quad (\mathbf B^T\mathbf P_A^{\perp})^{+} ]
\begin{bmatrix}
\mathbf e \\ \mathbf f
\end{bmatrix}
=
(\mathbf A^T\mathbf P_B^{\perp})^{+}\,\mathbf e
+
(\mathbf B^T\mathbf P_A^{\perp} )^{+}\,\mathbf f
.](../I/m/85b4e4390a1cc674d03de3945a698fed.png)