Bloch equations
In physics and chemistry, specifically in nuclear magnetic resonance (NMR), magnetic resonance imaging (MRI), and electron spin resonance (ESR), the Bloch equations are a set of macroscopic equations that are used to calculate the nuclear magnetization M = (Mx, My, Mz) as a function of time when relaxation times T1 and T2 are present. These are phenomenological equations that were introduced by Felix Bloch in 1946.[1] Sometimes they are called the equations of motion of nuclear magnetization. They are analogous to the Maxwell-Bloch equations.
Bloch equations in laboratory (stationary) frame of reference
Let M(t) = (Mx(t), My(t), Mz(t)) be the nuclear magnetization. Then the Bloch equations read:
where γ is the gyromagnetic ratio and B(t) = (Bx(t), By(t), B0 + ΔBz(t)) is the magnetic field experienced by the nuclei. The z component of the magnetic field B is sometimes composed of two terms:
- one, B0, is constant in time,
- the other one, ΔBz(t), may be time dependent. It is present in magnetic resonance imaging and helps with the spatial decoding of the NMR signal.
M(t) × B(t) is the cross product of these two vectors. M0 is the steady state nuclear magnetization (that is, for example, when t → ∞); it is in the z direction.
Physical background
With no relaxation (that is both T1 and T2 → ∞) the above equations simplify to:
or, in vector notation:
This is the equation for Larmor precession of the nuclear magnetization M in an external magnetic field B.
The relaxation terms,
represent an established physical process of transverse and longitudinal relaxation of nuclear magnetization M.
Bloch equations are macroscopic equations
These equations are not microscopic: they do not describe the equation of motion of individual nuclear magnetic moments. These are governed and described by laws of quantum mechanics.
Bloch equations are macroscopic: they describe the equations of motion of macroscopic nuclear magnetization that can be obtained by summing up all nuclear magnetic moment in the sample.
Alternative forms of Bloch equations
Opening the vector product brackets in the Bloch equations leads to:
The above form is further simplified assuming
where i = √(-1). After some algebra one obtains:
 .
.
where
 .
.
is the complex conjugate of Mxy. The real and imaginary parts of Mxy correspond to Mx and My respectively. Mxy is sometimes called transverse nuclear magnetization.
Matrix form of Bloch equations
The Bloch equations can be recast in matrix-vector notation:
Bloch equations in rotating frame of reference
In a rotating frame of reference, it is easier to understand the behaviour of the nuclear magnetization M. This is the motivation:
Solution of Bloch equations with T1, T2 → ∞
Assume that:
- at t = 0 the transverse nuclear magnetization Mxy(0) experiences a constant magnetic field B(t) = (0, 0, B0);
- B0 is positive;
- there are no longitudinal and transverse relaxations (that is T1 and T2 → ∞).
Then the Bloch equations are simplified to:
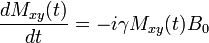 ,
, .
.
These are two (not coupled) linear differential equations. Their solution is:
 ,
,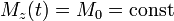 .
.
Thus the transverse magnetization, Mxy, rotates around the z axis with angular frequency ω0 = γB0 in clockwise direction (this is due to the negative sign in the exponent). The longitudinal magnetization, Mz remains constant in time. This is also how the transverse magnetization appears to an observer in the laboratory frame of reference (that is to a stationary observer).
Mxy(t) is translated in the following way into observable quantities of Mx(t) and My(t): Since
then
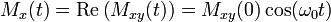 ,
, ,
,
where Re(z) and Im(z) are functions that return the real and imaginary part of complex number z. In this calculation it was assumed that Mxy(0) is a real number.
Transformation to rotating frame of reference
This is the conclusion of the previous section: in a constant magnetic field B0 along z axis the transverse magnetization Mxy rotates around this axis in clockwise direction with angular frequency ω0. If the observer were rotating around the same axis in clockwise direction with angular frequency Ω, Mxy it would appear to him rotating with angular frequency ω0 - Ω. Specifically, if the observer were rotating around the same axis in clockwise direction with angular frequency ω0, the transverse magnetization Mxy would appear to him stationary.
This can be expressed mathematically in the following way:
- Let (x, y, z) the Cartesian coordinate system of the laboratory (or stationary) frame of reference, and
- (x′, y′, z′) = (x′, y′, z) be a Cartesian coordinate system that is rotating around the z axis of the laboratory frame of reference with angular frequency Ω. This is called the rotating frame of reference. Physical variables in this frame of reference will be denoted by a prime.
Obviously:
 .
.
What is Mxy′(t)? Expressing the argument at the beginning of this section in a mathematical way:
 .
.
Equation of motion of transverse magnetization in rotating frame of reference
What is the equation of motion of Mxy′(t)?
Substitute from the Bloch equation in laboratory frame of reference:
But by assumption in the previous section: Bz′(t) = Bz(t) = B0 + ΔBz(t). Substituting into the equation above:
This is the meaning of terms on the right hand side of this equation:
- i (Ω - ω) Mxy′(t) is the Larmor term in the frame of reference rotating with angular frequency Ω. Note that it becomes zero when Ω = ω0.
- The -i γ ΔBz(t) Mxy′(t) term describes the effect of magnetic field inhomogeneity (as expressed by ΔBz(t)) on the transverse nuclear magnetization; it is used to explain T2*. It is also the term that is behind MRI: it is generated by the gradient coil system.
- The i γ ΔBxy′(t) Mz(t) describes the effect of RF field (the ΔBxy′(t) factor) on nuclear magnetization. For an example see below.
- - Mxy′(t) / T2 describes the loss of coherency of transverse magnetization.
Similarly, the equation of motion of Mz in the rotating frame of reference is:
Time independent form of the equations in the rotating frame of reference
When the external field has the form:
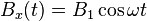

 ,
,
We define:
 and :
and : ,
,
and get (in the matrix-vector notation):
Simple solutions of Bloch equations
Relaxation of transverse nuclear magnetization Mxy
Assume that:
- The nuclear magnetization is exposed to constant external magnetic field in the z direction Bz′(t) = Bz(t) = B0. Thus ω0 = γB0 and ΔBz(t) = 0.
- There is no RF, that is Bxy' = 0.
- The rotating frame of reference rotates with an angular frequency Ω = ω0.
Then in the rotating frame of reference, the equation of motion for the transverse nuclear magnetization, Mxy'(t) simplifies to:
This is a linear ordinary differential equation and its solution is
 .
.
where Mxy'(0) is the transverse nuclear magnetization in the rotating frame at time t = 0. This is the initial condition for the differential equation.
Note that when the rotating frame of reference rotates exactly at the Larmor frequency (this is the physical meaning of the above assumption Ω = ω0), the vector of transverse nuclear magnetization, Mxy(t) appears to be stationary.
Relaxation of longitudinal nuclear magnetization Mz
Assume that:
- The nuclear magnetization is exposed to constant external magnetic field in the z direction Bz′(t) = Bz(t) = B0. Thus ω0 = γB0 and ΔBz(t) = 0.
- There is no RF, that is Bxy' = 0.
- The rotating frame of reference rotates with an angular frequency Ω = ω0.
Then in the rotating frame of reference, the equation of motion for the longitudinal nuclear magnetization, Mz(t) simplifies to:
This is a linear ordinary differential equation and its solution is
where Mz(0) is the longitudinal nuclear magnetization in the rotating frame at time t = 0. This is the initial condition for the differential equation.
90 and 180° RF pulses
Assume that:
- Nuclear magnetization is exposed to constant external magnetic field in z direction Bz′(t) = Bz(t) = B0. Thus ω0 = γB0 and ΔBz(t) = 0.
- At t = 0 an RF pulse of constant amplitude and frequency ω0 is applied. That is B'xy(t) = B'xy is constant. Duration of this pulse is τ.
- The rotating frame of reference rotates with an angular frequency Ω = ω0.
- T1 and T2 → ∞. Practically this means that τ ≪ T1 and T2.
Then for 0 ≤ t ≤ τ:
See also
- The Bloch–Torrey equation is a generalization of the Bloch equations, which includes added terms due to the transfer of magnetization by diffusion.[2]
References
- ↑ F Bloch, Nuclear Induction, Physical Review 70, 460-473 (1946)
- ↑ Torrey, H C (1956). "Bloch Equations with Diffusion Terms". Physical Review 104 (3): 563–565. Bibcode:1956PhRv..104..563T. doi:10.1103/PhysRev.104.563. (1956)
Further reading
- Charles Kittel, Introduction to Solid State Physics, John Wiley & Sons, 8th edition (2004), ISBN 978-0-471-41526-8. Chapter 13 is on Magnetic Resonance.


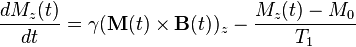




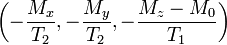





![M_{xy}(t) = M_{xy} (0) e^{-i \gamma B_{z0} t} = M_{xy} (0) \left [ \cos (\omega _0 t) - i \sin (\omega_0 t) \right ]](../I/m/faff6ad9b372f2e3743376e6394c8091.png)

![\begin{align} \frac {d M_{xy}'(t)} {d t} & = e^{+i \Omega t} \left [-i \gamma \left ( M_{xy} (t) B_z (t) - M_z (t) B_{xy} (t) \right ) -
\frac {M_{xy}} {T_2} \right ] + i \Omega M_{xy}' \\
& = \left [-i \gamma \left ( M_{xy} (t) e^{+i \Omega t} B_z (t) - M_z (t) B_{xy} (t) e^{+i \Omega t}\right ) -
\frac {M_{xy} e^{+i \Omega t} } {T_2} \right ] + i \Omega M_{xy}' \\
& = -i \gamma \left ( M_{xy}' (t) B_z' (t) - M_z' (t) B_{xy}' (t) \right ) + i \Omega M_{xy}' -
\frac {M_{xy}'} {T_2} \\
\end{align}](../I/m/d203faa6937256875d273c247e45f809.png)





![M_z(t) = M_{z,\mathrm{eq}} - [M_{z,\mathrm{eq}} - M_z(0)]e^{-t/T_1}](../I/m/5fbe47b5e577a0b83fa97f3677050256.png)

