Blaschke selection theorem
The Blaschke selection theorem is a result in topology and convex geometry about sequences of convex sets. Specifically, given a sequence 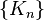 of convex sets contained in a bounded set, the theorem guarantees the existence of a subsequence
of convex sets contained in a bounded set, the theorem guarantees the existence of a subsequence 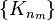 and a convex set
and a convex set  such that
such that 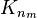 converges to
converges to  in the Hausdorff metric. The theorem is named for Wilhelm Blaschke.
in the Hausdorff metric. The theorem is named for Wilhelm Blaschke.
Alternate statements
- A succinct statement of the theorem is that a metric space of convex bodies is locally compact.
- Using the Hausdorff metric on sets, every infinite collection of compact subsets of the unit ball has a limit point (and that limit point is itself a compact set).
Application
As an example of its use, the isoperimetric problem can be shown to have a solution.[1] That is, there exists a curve of fixed length that encloses the maximum area possible. Other problems likewise can be shown to have a solution:
- Lebesgue universal cover problem for a convex universal cover of minimal size for the collection of all sets in the plane of unit diameter,[1]
- the maximum inclusion problem,[1]
- and the Moser's worm problem for a convex universal cover of minimal size for the collection of planar curves of unit length.[2]
Notes
- ↑ 1.0 1.1 1.2 Paul J. Kelly; Max L. Weiss (1979). Geometry and Convexity: A Study in Mathematical Methods. Wiley. pp. Section 6.4.
- ↑ Wetzel, John E. (July 2005). "The Classical Worm Problem --- A Status Report". Geombinatorics 15 (1): 34–42.
References
- A. B. Ivanov (2001), "Blaschke selection theorem", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- V. A. Zalgaller (2001), "Metric space of convex sets", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Kai-Seng Chou; Xi-Ping Zhu (2001). The Curve Shortening Problem. CRC Press. p. 45. ISBN 1-58488-213-1.