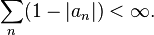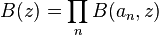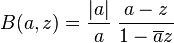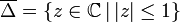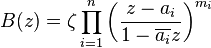Blaschke product
In complex analysis, the Blaschke product is a bounded analytic function in the open unit disc constructed to have zeros at a (finite or infinite) sequence of prescribed complex numbers
- a0, a1, ...
inside the unit disc.
Blaschke products were introduced by Wilhelm Blaschke (1915). They are related to Hardy spaces.
Definition
A sequence of points 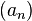 inside the unit disk is said to satisfy the Blaschke condition when
inside the unit disk is said to satisfy the Blaschke condition when
Given a sequence obeying the Blaschke condition, the Blaschke product is defined as
with factors
provided a ≠ 0. Here 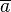 is the complex conjugate of a. When a = 0 take B(0,z) = z.
is the complex conjugate of a. When a = 0 take B(0,z) = z.
The Blaschke product B(z) defines a function analytic in the open unit disc, and zero exactly at the an (with multiplicity counted): furthermore it is in the Hardy class 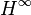 .[1]
.[1]
The sequence of an satisfying the convergence criterion above is sometimes called a Blaschke sequence.
Szegő theorem
A theorem of Gábor Szegő states that if f is in 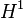 , the Hardy space with integrable norm, and if f is not identically zero, then the zeroes of f (certainly countable in number) satisfy the Blaschke condition.
, the Hardy space with integrable norm, and if f is not identically zero, then the zeroes of f (certainly countable in number) satisfy the Blaschke condition.
Finite Blaschke products
Finite Blaschke products can be characterized (as analytic functions on the unit disc) in the following way: Assume that f is an analytic function on the open unit disc such that f can be extended to a continuous function on the closed unit disc
which maps the unit circle to itself. Then ƒ is equal to a finite Blaschke product
where ζ lies on the unit circle and mi is the multiplicity of the zero ai, |ai| < 1. In particular, if ƒ satisfies the condition above and has no zeros inside the unit circle then ƒ is constant (this fact is also a consequence of the maximum principle for harmonic functions, applied to the harmonic function log(|ƒ(z)|)).
See also
- Hardy space
- Weierstrass product
References
- ↑ Conway (1996) 274
- W. Blaschke, Eine Erweiterung des Satzes von Vitali über Folgen analytischer Funktionen Berichte Math.-Phys. Kl., Sächs. Gesell. der Wiss. Leipzig, 67 (1915) pp. 194–200
- Peter Colwell, Blaschke Products — Bounded Analytic Functions (1985), University of Michigan Press, Ann Arbor. ISBN 0-472-10065-3
- Conway, John B.. Functions of a Complex Variable II. Graduate Texts in Mathematics 159. Springer-Verlag. pp. 273–274. ISBN 0-387-94460-5.
- Tamrazov, P.M. (2001), "b/b016630", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4