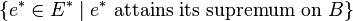Bishop–Phelps theorem
In mathematics, the Bishop–Phelps theorem is a theorem about the topological properties of Banach spaces named after Errett Bishop and Robert Phelps, who published its proof in 1961.
Its statement is as follows.
- Let B ⊂ E be a bounded, closed, convex set of a Banach space E. Then the set
- is norm-dense in the dual
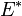 .
.
See also
References
- Bishop, Errett; Phelps, R. R. (1961). "A proof that every Banach space is subreflexive". Bulletin of the American Mathematical Society 67: 97–98. doi:10.1090/s0002-9904-1961-10514-4. MR 123174.
| ||||||||||||||||||||||||||||||||||