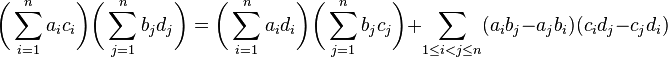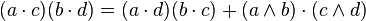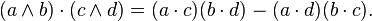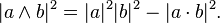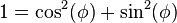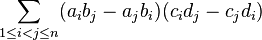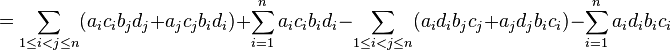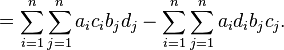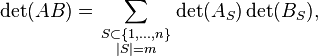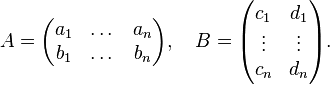Binet–Cauchy identity

In algebra, the Binet–Cauchy identity, named after Jacques Philippe Marie Binet and Augustin-Louis Cauchy, states that [1]

\biggl(\sum_{i=1}^n a_i c_i\biggr) \biggl(\sum_{j=1}^n b_j d_j\biggr) = \biggl(\sum_{i=1}^n a_i d_i\biggr) \biggl(\sum_{j=1}^n b_j c_j\biggr) + \sum_{1\le i < j \le n} (a_i b_j - a_j b_i ) (c_i d_j - c_j d_i )

for every choice of real or complex numbers (or more generally, elements of a commutative ring). Setting ai = ci and bj = dj, it gives the Lagrange's identity, which is a stronger version of the Cauchy–Schwarz inequality for the Euclidean space 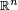\scriptstyle\mathbb{R}^n.

The Binet–Cauchy identity and exterior algebra

When n = 3 the first and second terms on the right hand side become the squared magnitudes of dot and cross products respectively; in n dimensions these become the magnitudes of the dot and wedge products. We may write it

(a \cdot c)(b \cdot d) = (a \cdot d)(b \cdot c) + (a \wedge b) \cdot (c \wedge d)\,

where a, b, c, and d are vectors. It may also be written as a formula giving the dot product of two wedge products, as

(a \wedge b) \cdot (c \wedge d) = (a \cdot c)(b \cdot d) - (a \cdot d)(b \cdot c).\,

In the special case of unit vectors a=c and b=d, the formula yields

|a \wedge b|^2 = |a|^2|b|^2 - |a \cdot b|^2. \,

When both vectors are unit vectors, we obtain the usual relation

1= \cos^2(\phi)+\sin^2(\phi)

where φ is the angle between the vectors.

Proof

Expanding the last term,

\sum_{1\le i < j \le n} (a_i b_j - a_j b_i ) (c_i d_j - c_j d_i )
= \sum_{1\le i < j \le n} (a_i c_i b_j d_j + a_j c_j b_i d_i) +\sum_{i=1}^n a_i c_i b_i d_i - \sum_{1\le i < j \le n} (a_i d_i b_j c_j + a_j d_j b_i c_i) - \sum_{i=1}^n a_i d_i b_i c_i

where the second and fourth terms are the same and artificially added to complete the sums as follows:

= \sum_{i=1}^n \sum_{j=1}^n a_i c_i b_j d_j - \sum_{i=1}^n \sum_{j=1}^n a_i d_i b_j c_j.

This completes the proof after factoring out the terms indexed by i.

Generalization

A general form, also known as the Cauchy–Binet formula, states the following: Suppose A is an m×n matrix and B is an n×m matrix. If S is a subset of {1, ..., n} with m elements, we write AS for the m×m matrix whose columns are those columns of A that have indices from S. Similarly, we write BS for the m×m matrix whose rows are those rows of B that have indices from S. Then the determinant of the matrix product of A and B satisfies the identity

\det(AB) = \sum_{\scriptstyle S\subset\{1,\ldots,n\}\atop\scriptstyle|S|=m} \det(A_S)\det(B_S),

where the sum extends over all possible subsets S of {1, ..., n} with m elements.

We get the original identity as special case by setting

A=\begin{pmatrix}a_1&\dots&a_n\\b_1&\dots& b_n\end{pmatrix},\quad B=\begin{pmatrix}c_1&d_1\\\vdots&\vdots\\c_n&d_n\end{pmatrix}.

In-line notes and references

  1. ↑ Eric W. Weisstein (2003). "Binet-Cauchy identity". CRC concise encyclopedia of mathematics (2nd ed.). CRC Press. p. 228. ISBN 1-58488-347-2.