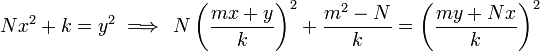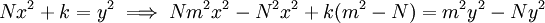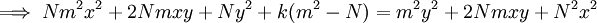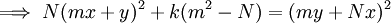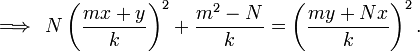Bhaskara's lemma
Bhaskara's Lemma is an identity used as a lemma during the chakravala method. It states that:
for integers 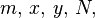 and non-zero integer
and non-zero integer 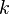 .
.
Proof
The proof follows from simple algebraic manipulations as follows: multiply both sides of the equation by 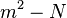 , add
, add 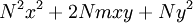 , factor, and divide by
, factor, and divide by 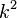 .
.
So long as neither 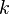 nor
nor 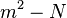 are zero, the implication goes in both directions. (Note also that the lemma holds for real or complex numbers as well as integers.)
are zero, the implication goes in both directions. (Note also that the lemma holds for real or complex numbers as well as integers.)
References
- C. O. Selenius, "Rationale of the chakravala process of Jayadeva and Bhaskara II", Historia Mathematica, 2 (1975), 167-184.
- C. O. Selenius, Kettenbruch theoretische Erklarung der zyklischen Methode zur Losung der Bhaskara-Pell-Gleichung, Acta Acad. Abo. Math. Phys. 23 (10) (1963).
- George Gheverghese Joseph, The Crest of the Peacock: Non-European Roots of Mathematics (1975).
External links
| ||||||||||||||||||||||||||||||||||||||