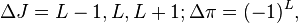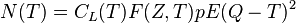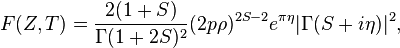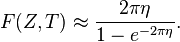Beta decay
| Nuclear physics |
|---|
 |
| Nucleus · Nucleons (p, n) · Nuclear force · Nuclear reaction |
|
Nuclear models and stability Liquid drop · Nuclear shell · Nuclear structure Binding energy · p–n ratio · Drip line · Stability Isl. |
|
Alpha α · Beta β (2β, β+) · K/L capture · Isomeric (Gamma γ · Internal conversion) · Spontaneous fission · Cluster decay · Neutron emission · Proton emission |
|
Nucleosynthesis topics Nuclear fusion Processes: Stellar · Big Bang · Supernova Nuclides: Primordial · Cosmogenic · Artificial |
|
Scientists |
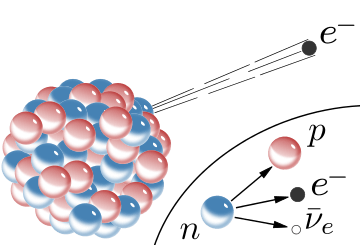
In nuclear physics, beta decay (β decay) is a type of radioactive decay in which a proton is transformed into a neutron, or vice versa, inside an atomic nucleus. This process allows the atom to move closer to the optimal ratio of protons and neutrons. As a result of this transformation, the nucleus emits a detectable beta particle, which is an electron or positron.[1]
Beta decay is mediated by the weak force. There are two types of beta decay, known as beta minus and beta plus. Beta minus (β−) decay produces an electron and electron antineutrino, while beta plus (β+) decay produces a positron and electron neutrino; β+ decay is thus also known as positron emission.[2]
An example of electron emission (β− decay) is the decay of carbon-14 into nitrogen-14:
- 14
6C → 14
7N + e− + ν
e
In this form of decay, the original element becomes a new chemical element in a process known as nuclear transmutation. This new element has an unchanged mass number A but an atomic number Z that is increased by one. As in all nuclear decays, the decaying element (in this case 14
6C) is known as the parent nuclide while the resulting element (in this case 14
7N) is known as the daughter nuclide. The emitted electron or positron is known as a beta particle.
An example of positron emission (β+ decay) is the decay of magnesium-23 into sodium-23:
- 23
12Mg → 23
11Na + e+ + ν
e
In contrast to β− decay, β+ decay is accompanied by the emission of an electron neutrino. β+ decay also results in nuclear transmutation, with the resulting element having an atomic number that is decreased by one.
Electron capture is sometimes included as a type of beta decay, because the basic nuclear process, mediated by the weak force, is the same. In electron capture, an inner atomic electron is captured by a proton in the nucleus, transforming it into a neutron, and an electron neutrino is released. An example of electron capture is the decay of krypton-81 into bromine-81:
- 81
36Kr + e− → 81
35Br + ν
e
Electron capture is a competing (simultaneous) decay process for all nuclei that can undergo β+ decay. The converse, however, is not true: electron capture is the only type of decay that is allowed in proton-rich nuclides that do not have sufficient energy to emit a positron and neutrino.[3]
β− decay

In β− decay, the weak interaction converts an atomic nucleus into a nucleus with atomic number increased by one, while emitting an electron (e−) and an electron antineutrino (ν
e).
The generic equation is:
- A
ZX → A
Z+1X’ + e− + ν
e [1]
where A and Z are the mass number and atomic number of the decaying nucleus, and X and X’ are the initial and final elements, respectively.
Another example is when the free neutron (1
0n) decays by β− decay into a proton (p):
- n → p + e− + ν
e.
At the fundamental level (as depicted in the Feynman diagram on the left), this is caused by the conversion of the negatively charged (−1⁄3 e) down quark to the positively charged (+2⁄3 e) up quark by emission of a W− boson; the W− boson subsequently decays into an electron and an electron antineutrino:
- d → u + e− + ν
e.
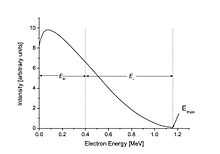
The beta spectrum is a continuous spectrum: the total decay energy is divided between the electron and the antineutrino. In the figure to the right, this is shown, by way of example, for an electron of 0.4 MeV energy. In this example, the antineutrino then gets the remainder: 0.76 MeV, since the total decay energy is assumed to be 1.16 MeV.
β− decay generally occurs in neutron-rich nuclei.[4]
β+ decay
In β+ decay, or "positron emission", the weak interaction converts an atomic nucleus into a nucleus with atomic number decreased by one, while emitting a positron (e+) and an electron neutrino (ν
e). The generic equation is:
- A
ZX → A
Z−1X’ + e+ + ν
e [1]
β+ decay cannot occur in an isolated proton because it requires energy due to the mass of the neutron being greater than the mass of the proton. β+ decay can only happen inside nuclei when the daughter nucleus has a greater binding energy (and therefore a lower total energy) than the mother nucleus. The difference between these energies goes into the reaction of converting a proton into a neutron, a positron and a neutrino and into the kinetic energy of these particles. In an opposite process to negative beta decay, the weak interaction converts a proton into a neutron by converting an up quark into a down quark by having it emit a W+ or absorb a W−.
Electron capture (K-capture)
In all cases where β+ decay of a nucleus is allowed energetically, the electron capture process is also allowed, in which the same nucleus captures an atomic electron with the emission of a neutrino:
- A
ZX + e− → A
Z−1X’ + ν
e
The emitted neutrino is mono-energetic. In proton-rich nuclei where the energy difference between initial and final states is less than 2mec2, β+ decay is not energetically possible, and electron capture is the sole decay mode.[3]
If the captured electron comes from the innermost shell of the atom, the K-shell, which has the highest probability to interact with the nucleus, the process is called K-capture.[5] If it comes from the L-shell, the process is called L-capture, etc.
Competition of beta decay types
Three types of beta decay in competition are illustrated by the single isotope copper-64 (29 protons, 35 neutrons), which has a half-life of about 12.7 hours. This isotope has one unpaired proton and one unpaired neutron, so either the proton or the neutron can decay. This particular nuclide (though not all nuclides in this situation) is almost equally likely to decay through proton decay by positron emission (18%) or electron capture (43%), as through neutron decay by electron emission (39%).
Helicity (polarization) of neutrinos, electrons and positrons emitted in beta decay
After the discovery of parity non-conservation (see history below), it was found that in beta decay, electrons are emitted mostly with negative helicity, i.e., they move, naively speaking, like left-handed screws driven into a material (they have negative longitudinal polarization).[6] Conversely, positrons have mostly positive helicity, i.e., they move like right-handed screws. Neutrinos (emitted in positron decay) have positive helicity, while antineutrinos (emitted in electron decay) have negative helicity.[7]
The higher the energy of the particles, the higher is their polarization.
Energy release
The Q value is defined as the total amount of energy released in a given nuclear decay. In beta decay, Q is therefore also the sum of the kinetic energies of the emitted beta particle, neutrino, and recoiling nucleus. (Because of the large mass of the nucleus compared to that of the beta particle and neutrino, the kinetic energy of the recoiling nucleus can generally be neglected.) Beta particles can therefore be emitted with any kinetic energy ranging from 0 to Q.[1] A typical Q is around 1 MeV, but can range from a few keV to a few tens of MeV.
Since the rest mass of the electron is 511 keV, the most energetic beta particles are ultrarelativistic, with speeds very close to the speed of light.
β− decay
Consider the generic equation for beta decay
- A
ZX → A
Z+1X’ + e− + ν
e.
The Q value for this decay is
![Q=\left[m_N\left({}^A_Z\mathrm{X}\right) - m_N\left({}^A_{Z+1}\mathrm{X'}\right)-m_e-m_{\overline\nu_e}\right]c^2](../I/m/7c207417923741d3779aba1d8021bdac.png) ,
,
where 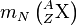 is the mass of the nucleus of the A
is the mass of the nucleus of the A
ZX atom, 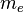 is the mass of the electron, and
is the mass of the electron, and 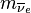 is the mass of the electron antineutrino. In other words, the total energy released is the mass energy of the initial nucleus, minus the mass energy of the final nucleus, electron, and antineutrino. The mass of the nucleus mN is related to the standard atomic mass m by
is the mass of the electron antineutrino. In other words, the total energy released is the mass energy of the initial nucleus, minus the mass energy of the final nucleus, electron, and antineutrino. The mass of the nucleus mN is related to the standard atomic mass m by
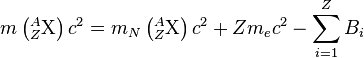 .
.
That is, the total atomic mass is the mass of the nucleus, plus the mass of the electrons, minus the binding energy Bi of each electron. Substituting this into our original equation, while neglecting the nearly-zero antineutrino mass and difference in electron binding energy, which is very small for high-Z atoms, we have
This energy is carried away as kinetic energy by the electron and neutrino.
Because the reaction will proceed only when the Q-value is positive, β− decay can occur when the mass of atom A
ZX is greater than the mass of atom A
Z+1X’.[8]
β+ decay
The equations for β+ decay are similar, with the generic equation
- A
ZX → A
Z−1X’ + e+ + ν
e
giving
![Q=\left[m_N\left({}^A_Z\mathrm{X}\right) - m_N\left({}^A_{Z-1}\mathrm{X'}\right)-m_e-m_{\nu_e}\right]c^2](../I/m/aa22e87317b6127c7dd9d42953aad2b4.png) .
.
However, in this equation, the electron masses do not cancel, and we are left with
Because the reaction will proceed only when the Q-value is positive, β+ decay can occur when the mass of atom A
ZX exceeds that of A
Z-1X’ by at least twice the mass of the electron.[8]
Electron capture
The analogous calculation for electron capture must take into account the binding energy of the electrons. This is because the atom will be left in an excited state after capturing the electron, and the binding energy of the captured innermost electron is significant. Using the generic equation for electron capture
- A
ZX + e− → A
Z−1X’ + ν
e
we have
![Q=\left[m_N\left({}^A_Z\mathrm{X}\right) + m_e - m_N\left({}^A_{Z-1}\mathrm{X'}\right)-m_{\nu_e}\right]c^2](../I/m/a0d55c44f6167fbc42acfee5557f93fa.png) ,
,
which simplifies to
![Q=\left[m\left({}^A_Z\mathrm{X}\right) - m\left({}^A_{Z-1}\mathrm{X'}\right)\right]c^2-B_n](../I/m/34b08fe760742935a6e848322ba8a905.png) ,
,
where Bn is the binding energy of the captured electron.
Because the binding energy of the electron is much less than the mass of the electron, nuclei that can undergo β+ decay can always also undergo electron capture, but the reverse is not true.[8]
Nuclear transmutation

If the proton and neutron are part of an atomic nucleus, these decay processes transmute one chemical element into another. For example:
137
55Cs→ 137
56Ba+ e− + ν
e(beta minus decay) 22
11Na→ 22
10Ne+ e+ + ν
e(beta plus decay) 22
11Na+ e− → 22
10Ne+ ν
e(electron capture)
Beta decay does not change the number A of nucleons in the nucleus but changes only its charge Z. Thus the set of all nuclides with the same A can be introduced; these isobaric nuclides may turn into each other via beta decay. Among them, several nuclides (at least one for any given mass number A) are beta stable, because they present local minima of the mass excess: if such a nucleus has (A, Z) numbers, the neighbour nuclei (A, Z−1) and (A, Z+1) have higher mass excess and can beta decay into (A, Z), but not vice versa. For all odd mass numbers A, there is only one known beta-stable isobar. For even A, there are up to three different beta-stable isobars experimentally known; for example, 96
40Zr, 96
42Mo, and 96
44Ru are all beta-stable. There are about 355 known beta-decay stable nuclides total.[9]
Usually unstable nuclides are clearly either "neutron rich" or "proton rich", with the former undergoing beta decay and the latter undergoing electron capture (or more rarely, due to the higher energy requirements, positron decay). However, in a few cases of odd-proton, odd-neutron radionuclides, it may be energetically favorable for the radionuclide to decay to an even-proton, even-neutron isobar either by undergoing beta-positive or beta-negative decay. An often-cited example is 64
29Cu, which decays by positron emission 61% of the time to 64
28Ni, and 39% of the time by (negative) beta decay to 64
30Zn.[10]
Most naturally occurring isotopes on Earth are beta stable. Those that are not have half-lives ranging from under a second to periods of time significantly greater than the age of the universe. One common example of a long-lived isotope is the odd-proton odd-neutron nuclide 40
19K, which undergoes all three types of beta decay (β−, β+ and electron capture) with a half-life of 1.277×109 years.[11]
Double beta decay
Some nuclei can undergo double beta decay (ββ decay) where the charge of the nucleus changes by two units. Double beta decay is difficult to study, as the process has an extremely long half-life. In nuclei for which both β decay and ββ decay are possible, the rarer ββ decay process is effectively impossible to observe. However, in nuclei where β decay is forbidden but ββ decay is allowed, the process can be seen and a half-life measured.[12] Thus, ββ decay is usually studied only for beta stable nuclei. Like single beta decay, double beta decay does not change A; thus, at least one of the nuclides with some given A has to be stable with regard to both single and double beta decay.
"Ordinary" double beta decay results in the emission of two electrons and two antineutrinos. If neutrinos are Majorana particles (i.e., they are their own antiparticles), then a decay known as neutrinoless double beta decay will occur. Most neutrino physicists believe that neutrinoless double beta decay has never been observed.[12]
Bound-state β− decay
A very small minority of free neutron decays (about four per million) are so-called "two-body decays", in which the proton, electron and antineutrino are produced, but the electron fails to gain the 13.6 eV necessary energy to escape the proton, and therefore simply remains bound to it, as a neutral hydrogen atom.[13] In this type of beta decay, in essence all of the neutron decay energy is carried off by the antineutrino.
For fully ionized atoms (bare nuclei), it is possible in likewise manner for electrons to fail to escape the atom, and to be emitted from the nucleus into low-lying atomic bound states (orbitals). This can not occur for neutral atoms whose low-lying bound states are already filled by electrons.
The phenomenon in fully ionized atoms was first observed for 163Dy66+ in 1992 by Jung et al. of the Darmstadt Heavy-Ion Research group. Although neutral 163Dy is a stable isotope, the fully ionized 163Dy66+ undergoes β decay into the K and L shells with a half-life of 47 days.[14]
Another possibility is that a fully ionized atom undergoes greatly accelerated β decay, as observed for 187Re by Bosch et al., also at Darmstadt. Neutral 187Re does undergo β decay with a half-life of 42 × 109 years, but for fully ionized 187Re75+ this is shortened by a factor of 109 to only 32.9 years.[15] For comparison the variation of decay rates of other nuclear processes due to chemical environment is less than 1%.
Forbidden transitions
Beta decays can be classified according to the L-value of the emitted radiation. When L > 0, the decay is referred to as "forbidden". Nuclear selection rules require high L-values to be accompanied by changes in nuclear spin (J) and parity (π). The selection rules for the Lth forbidden transitions are:
where Δπ = 1 or −1 corresponds to no parity change or parity change, respectively. The special case of a 0+ → 0+ transition (which in gamma decay is absolutely forbidden) is referred to as "superallowed" for beta decay, and proceeds very quickly by this decay route. (It competes with internal conversion for decay of excited nuclei where the ratio of neutrons to protons does not favor a beta decay in either direction). The following table lists the ΔJ and Δπ values for the first few values of L:
| Forbiddenness | ΔJ | Δπ |
|---|---|---|
| Superallowed | 0+ → 0+ | no |
| Allowed | 0, 1 | no |
| First forbidden | 0, 1, 2 | yes |
| Second forbidden | 1, 2, 3 | no |
| Third forbidden | 2, 3, 4 | yes |
Beta emission spectrum

Beta decay can be considered as a perturbation as described in quantum mechanics, and thus Fermi's Golden Rule can be applied. This leads to an expression for the kinetic energy spectrum N(T) of emitted betas as follows:[16]
where T is the kinetic energy, CL is a shape function that depends on the forbiddenness of the decay (it is constant for allowed decays), F(Z, T) is the Fermi Function (see below) with Z the charge of the final-state nucleus, E = T + mc2 is the total energy, p =√(E/c)2 − (mc)2 is the momentum, and Q is the Q value of the decay. The kinetic energy of the emitted neutrino is given approximately by Q minus the kinetic energy of the beta.
As an example, the beta decay spectrum of 210Bi (originally called RaE) is shown to the right.
Fermi function
The Fermi function that appears in the beta spectrum formula accounts for the Coulomb attraction / repulsion between the emitted beta and the final state nucleus. Approximating the associated wavefunctions to be spherically symmetric, the Fermi function can be analytically calculated to be:[17]
where S =√1 − α2 Z2 (α is the fine-structure constant), η = ± αZE/pc (+ for electrons, − for positrons), ρ = rN/ℏ (rN is the radius of the final state nucleus), and Γ is the Gamma function.
For non-relativistic betas (Q ≪ mec2), this expression can be approximated by:[18]
Other approximations can be found in the literature.[19][20]
Kurie plot
A Kurie plot (also known as a Fermi–Kurie plot) is a graph used in studying beta decay developed by Franz N. D. Kurie, in which the square root of the number of beta particles whose momenta (or energy) lie within a certain narrow range, divided by the Fermi function, is plotted against beta-particle energy.[21][22] It is a straight line for allowed transitions and some forbidden transitions, in accord with the Fermi beta-decay theory. The energy-axis (x-axis) intercept of a Kurie plot corresponds to the maximum energy imparted to the electron/positron (the decay's Q-value). With Kurie plot one can find the limit on effective mass of neutrino.[23]
History
Discovery and characterization of β− decay
Radioactivity was discovered in 1896 by Henri Becquerel in uranium, and subsequently observed by Marie and Pierre Curie in thorium and in the new elements polonium and radium. In 1899, Ernest Rutherford separated radioactive emissions into two types: alpha and beta (now beta minus), based on penetration of objects and ability to cause ionization. Alpha rays could be stopped by thin sheets of paper or aluminium, whereas beta rays could penetrate several millimetres of aluminium. (In 1900, Paul Villard identified a still more penetrating type of radiation, which Rutherford identified as a fundamentally new type in 1903, and termed gamma rays).
In 1900, Becquerel measured the mass-to-charge ratio (m/e) for beta particles by the method of J.J. Thomson used to study cathode rays and identify the electron. He found that m/e for a beta particle is the same as for Thomson's electron, and therefore suggested that the beta particle is in fact an electron.
In 1901, Rutherford and Frederick Soddy showed that alpha and beta radioactivity involves the transmutation of atoms into atoms of other chemical elements. In 1913, after the products of more radioactive decays were known, Soddy and Kazimierz Fajans independently proposed their radioactive displacement law, which states that beta (i.e., β−) emission from one element produces another element one place to the right in the periodic table, while alpha emission produces an element two places to the left.
Neutrinos in beta decay
Historically, the study of beta decay provided the first physical evidence of the neutrino. Measurements of the beta decay spectrum in 1911 by Lise Meitner and Otto Hahn and in 1913 by Jean Danysz showed multiple lines on a diffuse background, offering the first hint of a continuous spectrum.[24] In 1914, James Chadwick used a magnetic spectrometer with one of Hans Geiger's new counters to make a more accurate measurement and showed that the spectrum was continuous.[24][25] This was in apparent contradiction to the law of conservation of energy, as it appeared that energy was lost in the beta decay process. A second problem was that the spin of the nitrogen-14 atom was an integer, in contradiction to the Rutherford prediction.
In 1920–1927, Charles Drummond Ellis (along with James Chadwick and colleagues) further established that the beta decay spectrum is continuous, ending all controversies. It also had an effective upper bound in energy, which was a severe blow to Bohr's suggestion that conservation of energy might be true only in a statistical sense, and might be violated in any given decay. Now the problem of how to account for the variability of energy in known beta decay products, as well as for conservation of momentum and angular momentum in the process, became acute.
In a famous letter written in 1930, Wolfgang Pauli suggested that in addition to electrons and protons atomic nuclei also contained an extremely light neutral particle which he called the neutron. He suggested that this "neutron" was also emitted during beta decay (thus accounting for the known missing energy, momentum, and angular momentum) and had simply not yet been observed. In 1931, Enrico Fermi renamed Pauli's "neutron" to neutrino, and in 1934, Fermi published a very successful model of beta decay in which neutrinos were produced. The neutrino interaction with matter was so weak that detecting it proved a severe experimental challenge which was finally met in 1956 in the Cowan–Reines neutrino experiment.[26] However, the properties of neutrinos were (with a few minor modifications) as predicted by Pauli and Fermi.
Non-conservation of parity
In 1956, Chien-Shiung Wu and coworkers proved in the Wu experiment that parity is not conserved in beta decay.[27][28] This surprising fact had been postulated shortly before in an article by Tsung-Dao Lee and Chen Ning Yang.[29]
Discovery of other types of beta decay
In 1934, Frédéric and Irène Joliot-Curie bombarded aluminium with alpha particles to effect the nuclear reaction 4
2He + 27
13Al → 30
15P + 1
0n, and observed that the product isotope 30
15P emits a positron identical to those found in cosmic rays by Carl David Anderson in 1932. This was the first example of β+ decay (positron emission), which they termed artificial radioactivity since 30
15P is a short-lived nuclide which does not exist in nature.
The theory of electron capture was first discussed by Gian-Carlo Wick in a 1934 paper, and then developed by Hideki Yukawa and others. K-electron capture was first observed in 1937 by Luis Alvarez, in the nuclide 48V.[30][31][32] Alvarez went on to study electron capture in 67Ga and other nuclides.[30][33][34]
See also
- Double beta decay
- Electron capture
- Neutrino
- Alpha decay
- Betavoltaics
- Particle radiation
- Radionuclide
- Tritium illumination, a form of fluorescent lighting powered by beta decay
- Pandemonium effect
- Total absorption spectroscopy
References
- Tuli, J. K. (2011). Nuclear Wallet Cards (PDF) (8th ed.). Brookhaven National Laboratory.
- ↑ 1.0 1.1 1.2 1.3 Konya, J.; Nagy, N. M. (2012). Nuclear and Radiochemistry. Elsevier. pp. 74–75. ISBN 978-0-12-391487-3.
- ↑ Basdevant, Jean-Louis; Rich, James; Spiro, Michael (2005). Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology. Springer. ISBN 978-0387016726.
- ↑ 3.0 3.1 Zuber, Kai (2011). Neutrino Physics (2 ed.). CRC Press. p. 466. ISBN 9781420064711.
- ↑ Loveland, Walter D. (2005). Modern Nuclear Chemistry. Wiley. p. 232. ISBN 0471115320.
- ↑ Tatjana Jevremovic (21 April 2009). Nuclear Principles in Engineering. Springer Science & Business Media. p. 201. ISBN 978-0-387-85608-7.
- ↑ H. Frauenfelder, R. Bobone, E. Von Goeler, N. Levine, H. R. Lewis, R. N. Peacock, A. Rossi and G. DePasquali, Physical Review 106 (1957) 386
- ↑ E. J. Konopinski and M. E. Rose, The Theory of nuclear Beta Decay, in: Alpha-, Beta- and Gamma-Ray Spectroscopy, ed. by Kai Siegbahn, Vol. 2, North-Holland Publishing Company, Amsterdam, 1966
- ↑ 8.0 8.1 8.2 Kenneth S. Krane (5 November 1987). Introductory Nuclear Physics. Wiley. ISBN 978-0-471-80553-3.
- ↑ "Interactive Chart of Nuclides". National Nuclear Data Center, Brookhaven National Laboratory. Retrieved 2014-09-18.
- ↑ "WWW Table of Radioactive Isotopes, Copper 64". LBNL Isotopes Project. Lawrence Berkeley National Laboratory. Retrieved 2014-09-18.
- ↑ "WWW Table of Radioactive Isotopes, Potassium 40". LBNL Isotopes Project. Lawrence Berkeley National Laboratory. Retrieved 2014-09-18.
- ↑ 12.0 12.1 S.M. Bilenky (October 5, 2010). "Neutrinoless double beta-decay". Physics of Particles and Nuclei 41 (5). doi:10.1134/S1063779610050035.
- ↑ An Overview Of Neutron Decay J. Byrne in Quark-Mixing, CKM Unitarity (H.Abele and D.Mund, 2002), see p.XV
- ↑ Jung, M. et al. (1992). "First observation of bound-state β− decay". Physical Review Letters 69 (15): 2164–2167. Bibcode:1992PhRvL..69.2164J. doi:10.1103/PhysRevLett.69.2164. PMID 10046415.
- ↑ Bosch, F. et al. (1996). "Observation of bound-state beta minus decay of fully ionized 187Re: 187Re–187Os Cosmochronometry". Physical Review Letters 77 (26): 5190–5193. Bibcode:1996PhRvL..77.5190B. doi:10.1103/PhysRevLett.77.5190. PMID 10062738.
- ↑ Nave, C. R. "Energy and Momentum Spectra for Beta Decay". HyperPhysics. Retrieved 2013-03-09.
- ↑ Fermi, E. (1934). "Versuch einer Theorie der β-Strahlen. I". Zeitschrift für Physik 88 (3–4): 161–177. Bibcode:1934ZPhy...88..161F. doi:10.1007/BF01351864.
- ↑ Mott, N. F.; Massey, H. S. W. (1933). The Theory of Atomic Collisions. Clarendon Press. LCCN 34001940.
- ↑ Venkataramaiah, P.; Gopala, K.; Basavaraju, A.; Suryanarayana, S. S.; Sanjeeviah, H. (1985). "A simple relation for the Fermi function". Journal of Physics G 11 (3): 359–364. Bibcode:1985JPhG...11..359V. doi:10.1088/0305-4616/11/3/014.
- ↑ Schenter, G. K.; Vogel, P. (1983). "A simple approximation of the fermi function in nuclear beta decay". Nuclear Science and Engineering 83 (3): 393–396. OSTI 5307377.
- ↑ Kurie, F. N. D.; Richardson, J. R.; Paxton, H. C. (1936). "The Radiations Emitted from Artificially Produced Radioactive Substances. I. The Upper Limits and Shapes of the β-Ray Spectra from Several Elements". Physical Review 49 (5): 368–381. Bibcode:1936PhRv...49..368K. doi:10.1103/PhysRev.49.368.
- ↑ Kurie, F. N. D. (1948). "On the Use of the Kurie Plot". Physical Review 73 (10): 1207. Bibcode:1948PhRv...73.1207K. doi:10.1103/PhysRev.73.1207.
- ↑ Rodejohann, Werner (2012). "Neutrinoless double beta decay and neutrino physics". 2. arXiv:1206.2560.
- ↑ 24.0 24.1 Jensen, Carsten (2000). Controversy and Consensus: Nuclear Beta Decay 1911-1934. Birkhäuser Verlag. ISBN 3-7643-5313-9.
- ↑ Chadwick, James (1914). "Intensitätsverteilung im magnetischen Spektren der β-Strahlen von Radium B + C". Verhandlungen der Deutschen Physikalischen Gesellschaft (in German) (Deutsche Physikalische Gesellschaft) 16: 383–391.
- ↑ C. L Cowan Jr., F. Reines, F. B. Harrison, H. W. Kruse, A. D McGuire (July 20, 1956). "Detection of the Free Neutrino: a Confirmation". Science 124 (3212): 103–4. Bibcode:1956Sci...124..103C. doi:10.1126/science.124.3212.103. PMID 17796274.
- ↑ C. S. Wu; E. Ambler; R. W. Hayward; D. D. Hoppes; R. P. Hudson (1957). "Experimental Test of Parity Conservation in Beta Decay". Physical Review 105: 1413–1415. doi:10.1103/PhysRev.105.1413.
- ↑ http://blogs.scientificamerican.com/guest-blog/2013/10/15/channeling-ada-lovelace-chien-shiung-wu-courageous-hero-of-physics/
- ↑ T. D. Lee, C. N. Yang (1956). "Question of Parity Conservation in Weak Interactions". Physical Review 104: 254–258. doi:10.1103/PhysRev.104.254.
- ↑ 30.0 30.1 Segré, E. (1987). "K-Electron Capture by Nuclei". In Trower, P. W. Discovering Alvarez: Selected Works of Luis W. Alvarez. University of Chicago Press. pp. 11–12. ISBN 978-0-226-81304-2.
- ↑ "The Nobel Prize in Physics 1968: Luis Alvarez". The Nobel Foundation. Retrieved 2009-10-07.
- ↑ Alvarez, L. W. (1937). "Nuclear K Electron Capture". Physical Review 52 (2): 134–135. Bibcode:1937PhRv...52..134A. doi:10.1103/PhysRev.52.134.
- ↑ Alvarez, L. W. (1938). "Electron Capture and Internal Conversion in Gallium 67". Physical Review 53 (7): 606. Bibcode:1938PhRv...53..606A. doi:10.1103/PhysRev.53.606.
- ↑ Alvarez, L. W. (1938). "The Capture of Orbital Electrons by Nuclei". Physical Review 54 (7): 486–497. Bibcode:1938PhRv...54..486A. doi:10.1103/PhysRev.54.486.
Bibliography
- Sin-Itiro Tomonaga (1997). The Story of Spin. University of Chicago Press.
External links
-
 The Live Chart of Nuclides - IAEA with filter on decay type
The Live Chart of Nuclides - IAEA with filter on decay type - Definition of Beta Disintegration (Decay) at Science Dictionary
| ||||||||||||||||||||
![Q=\left[m\left({}^A_Z\mathrm{X}\right)-m\left({}^A_{Z+1}\mathrm{X'}\right)\right]c^2](../I/m/2dd05e4052aab6c5495d26c973d06476.png)
![Q=\left[m\left({}^A_Z\mathrm{X}\right)-m\left({}^A_{Z-1}\mathrm{X'}\right)-2m_e\right]c^2](../I/m/97f337390e4022726e21d065b18a3a95.png)