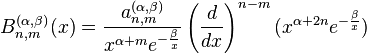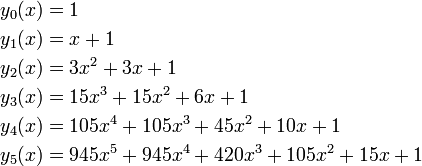Bessel polynomials
In mathematics, the Bessel polynomials are an orthogonal sequence of polynomials. There are a number of different but closely related definitions. The definition favored by mathematicians is given by the series (Krall & Frink, 1948)
Another definition, favored by electrical engineers, is sometimes known as the reverse Bessel polynomials (See Grosswald 1978, Berg 2000).
The coefficients of the second definition are the same as the first but in reverse order. For example, the third-degree Bessel polynomial is
while the third-degree reverse Bessel polynomial is
The reverse Bessel polynomial is used in the design of Bessel electronic filters.
Properties
Definition in terms of Bessel functions
The Bessel polynomial may also be defined using Bessel functions from which the polynomial draws its name.
where Kn(x) is a modified Bessel function of the second kind and yn(x) is the reverse polynomial (pag 7 and 34 Grosswald 1978).
Definition as a hypergeometric function
The Bessel polynomial may also be defined as a confluent hypergeometric function (Dita, 2006)
The reverse Bessel polynomial may be defined as a generalized Laguerre polynomial:
from which it follows that it may also be defined as a hypergeometric function:
where (−2n)n is the Pochhammer symbol (rising factorial).
The inversion for monomials is given by
Generating function
The Bessel polynomials have the generating function
Recursion
The Bessel polynomial may also be defined by a recursion formula:
and
Differential equation
The Bessel polynomial obeys the following differential equation:
and
Generalization
Explicit Form
A generalization of the Bessel polynomials have been suggested in literature (Krall, Fink), as following:
the corresponding reverse polynomials are
For the weighting function
they are orthogonal, for the relation
holds for m ≠ n and c a curve surrounding the 0 point.
They specialize to the Bessel polynomials for α = β = 2, in which situation ρ(x) = exp(−2 / x).
Rodrigues formula for Bessel polynomials
The Rodrigues formula for the Bessel polynomials as particular solutions of the above differential equation is :
where a(α, β)
n are normalization coefficients.
Associated Bessel polynomials
According to this generalization we have the following generalized differential equation for associated Bessel polynomials:
where 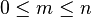 . The solutions are,
. The solutions are,
Particular values
none of which factor. Filaseta and Trifonov (Journal for Pure and Applied Mathematics, 550:125-140, 2002) proved that all Bessel polynomials are irreducible.
References
- Carlitz, Leonard (1957). "A Note on the Bessel Polynomials". Duke Math. J. 24 (2): 151–162. doi:10.1215/S0012-7094-57-02421-3. MR 0085360.
- Krall, H. L.; Frink, O. (1948). "A New Class of Orthogonal Polynomials: The Bessel Polynomials". Trans. Amer. Math. Soc. 65 (1): 100–115. doi:10.2307/1990516. JSTOR 1990516.
- Sloane, N. J. A. "The On-Line Encyclopedia of Integer Sequences". (See sequences
 A001497,
A001497,  A001498, and
A001498, and  A104548)
A104548) - Dita, P.; Grama, Grama, N. (May 24 2006). "On Adomian’s Decomposition Method for Solving Differential Equations". arXiv:solv-int/9705008 [solv-int]. Check date values in:
|date=(help) - Fakhri, H.; Chenaghlou, A. (2006). "Ladder operators and recursion relations for the associated Bessel polynomials". Physics Letters A 358 (5–6): 345–353. Bibcode:2006PhLA..358..345F. doi:10.1016/j.physleta.2006.05.070.
- Grosswald, E. (1978). Bessel Polynomials (Lecture Notes in Mathematics). New York: Springer. ISBN 0-387-09104-1.
- Roman, S. (1984). The Umbral Calculus (The Bessel Polynomials §4.1.7). New York: Academic Press. ISBN 0-486-44139-3.
- Berg, Christian; Vignat, C. (2000). "Linearization coefficients of Bessel polynomials and properties of Student-t distributions" (PDF). Retrieved 2006-08-16.
External links
- Hazewinkel, Michiel, ed. (2001), "Bessel polynomials", Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Weisstein, Eric W., "Bessel Polynomial", MathWorld.
- "Sloane's A001498 : Coefficients of Bessel polynomials", The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
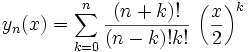
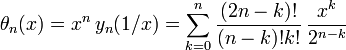
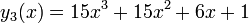
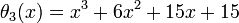
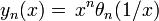
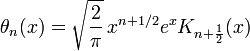
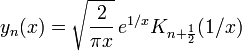
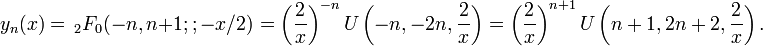
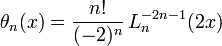
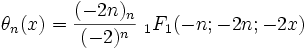
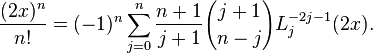
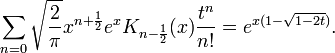
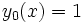
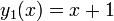
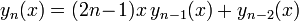
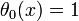
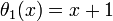
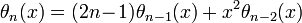
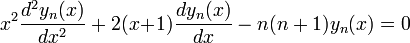
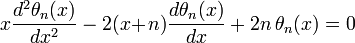
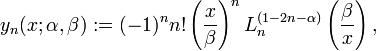
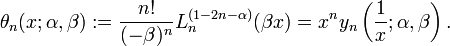
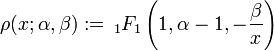
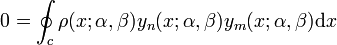
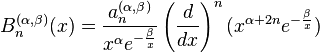
![x^2\frac{d^2B_{n,m}^{(\alpha,\beta)}(x)}{dx^2} + [(\alpha+2)x+\beta]\frac{dB_{n,m}^{(\alpha,\beta)}(x)}{dx} - \left[ n(\alpha+n+1) + \frac{m \beta}{x} \right] B_{n,m}^{(\alpha,\beta)}(x)=0](../I/m/d6e269bf07c628a60534ae0ccf781e4f.png)