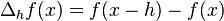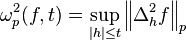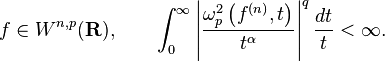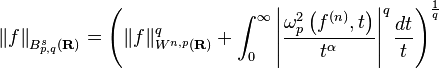Besov space

In mathematics, the Besov space (named after Oleg Vladimirovich Besov) 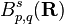B^s_{p,q}(\mathbf{R}) is a complete quasinormed space which is a Banach space when 1 ≤ p, q ≤ ∞. It, as well as the similarly defined Triebel–Lizorkin space, serve to generalize more elementary function spaces and are effective at measuring (in a sense) smoothness properties of functions.

Definition

Let

\Delta_h f(x) = f(x-h) - f(x)

and define the modulus of continuity by

\omega^2_p(f,t) = \sup_{|h| \le t} \left \| \Delta^2_h f \right \|_p

Let n be a non-negative integer and define: s = n + α with 0 < α ≤ 1. The Besov space 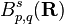B^s_{p,q}(\mathbf{R}) contains all functions f such that

f \in W^{n, p}(\mathbf{R}), \qquad \int_0^\infty \left|\frac{ \omega^2_p \left ( f^{(n)},t \right ) } {t^{\alpha} }\right|^q \frac{dt}{t} < \infty.

Norm

The Besov space 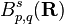B^s_{p,q}(\mathbf{R}) is equipped with the norm

\left \|f \right \|_{B^s_{p,q}(\mathbf{R})} = \left( \|f\|_{W^{n, p} (\mathbf{R})}^q + \int_0^\infty \left|\frac{ \omega^2_p \left ( f^{(n)}, t \right ) } {t^{\alpha} }\right|^q \frac{dt}{t} \right)^{\frac{1}{q}}

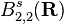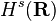The Besov spaces B^s_{2,2}(\mathbf{R}) coincide with the more classical Sobolev spaces H^s(\mathbf{R}).

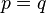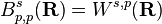If p=q then B^s_{p,p}(\mathbf{R}) =W^{s,p}( \mathbf{R}).

References